Appendix

Point group flowchart

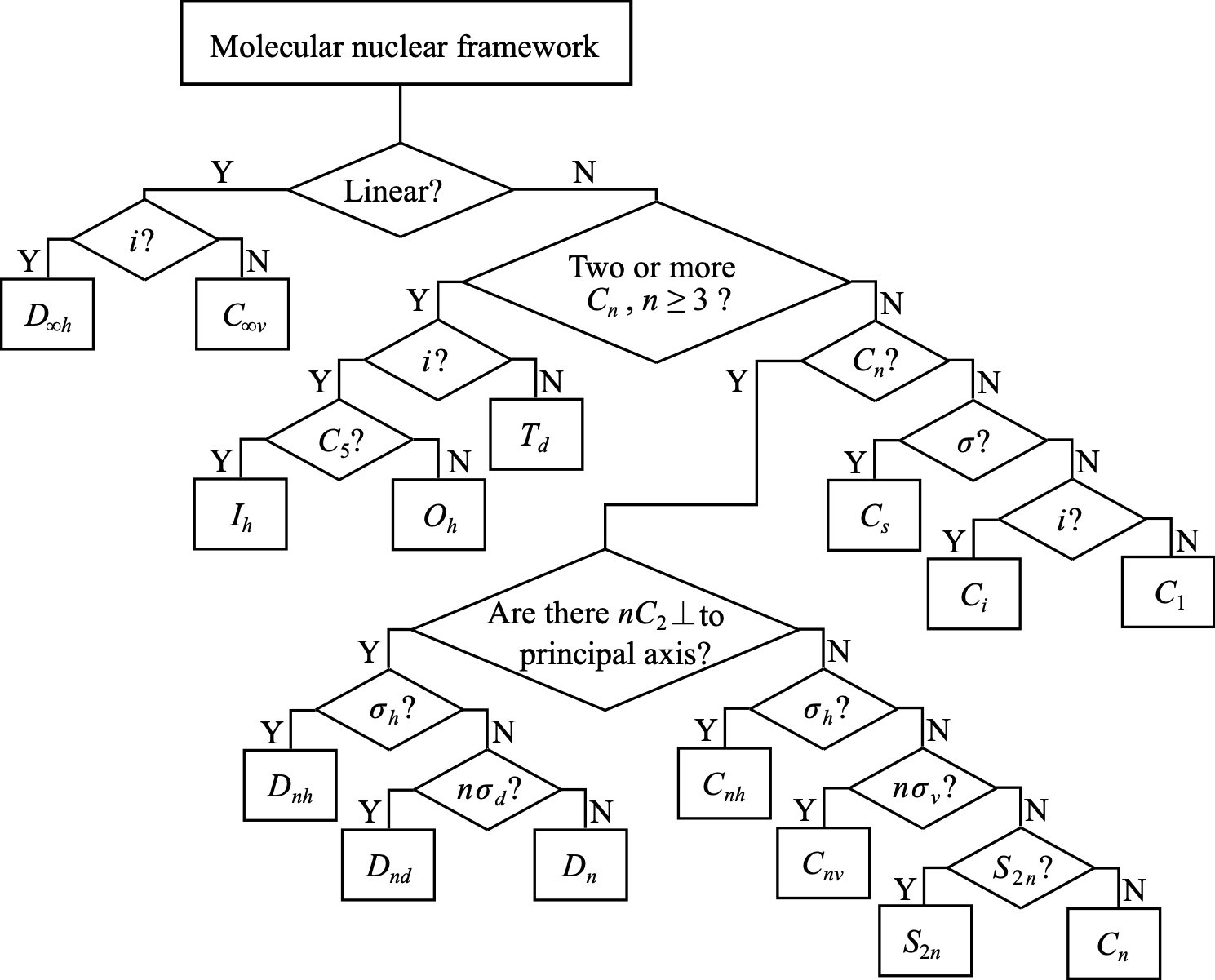
Fig. 1 Flowchart for the determination of molecular point groups.

Character tables

C\(_{2h}\)

Table 1 Character table for the \(C_{2h}\) point group.

Irrep	\(\hat{E}\)	\(\hat{C}_2(z)\)	\(\hat{i}\)	\(\hat{\sigma}_h\)	Operation
\(A_g\)	1	1	1	1	\(R_z\), \(x^2\), \(y^2\), \(z^2\)
\(B_{g}\)	1	-1	1	-1	\(R_x\), \(R_y\)
\(A_{u}\)	1	1	-1	-1	\(z\)
\(B_{u}\)	1	-1	-1	1	\(x\), \(y\)

D\(_{2h}\)

Table 2 Character table for the \(D_{2h}\) point group.

Irrep	\(\hat{E}\)	\(\hat{C}_2(z)\)	\(\hat{C}_2(y)\)	\(\hat{C}_2(x)\)	\(\hat{i}\)	\(\hat{\sigma}(xy)\)	\(\hat{\sigma}(xz)\)	\(\hat{\sigma}(yz)\)	Operation
\(A_g\)	1	1	1	1	1	1	1	1	\(x^2\), \(y^2\), \(z^2\)
\(B_{1g}\)	1	1	-1	-1	1	1	-1	-1	\(R_z\), \(xy\)
\(B_{2g}\)	1	-1	1	-1	1	-1	1	-1	\(R_y\), \(xz\)
\(B_{3g}\)	1	-1	-1	1	1	-1	-1	1	\(R_x\), \(yz\)
\(A_{u}\)	1	1	1	1	-1	-1	-1	-1
\(B_{1u}\)	1	1	-1	-1	-1	-1	1	1	\(z\)
\(B_{2u}\)	1	-1	1	-1	-1	1	-1	1	\(y\)
\(B_{3u}\)	1	-1	-1	1	-1	1	1	-1	\(x\)

Atomic units

A central problem in molecular physics is to solve the time-independent Schrödinger equation for the electrons in the field of the nuclei. Most often atomic units are then adopted. For the hydrogen atom, we have

\[ \left[ - \frac{\hbar^2}{2 m_\mathrm{e}} \nabla^2 - \frac{e^2}{4\pi\varepsilon_0 r} \right] \psi(\mathbf{r}) = E \psi(\mathbf{r}) \]

where \(\hbar\) is the reduced Planck constant, \(m_\mathrm{e}\) is the electron mass, \(e\) is the elementary charge, and \(\varepsilon_0\) is the electric constant. To cast this equation into dimensionless form, consider a coordinate transformation of the form

\[ \mathbf{r} = (x,y,z) \longrightarrow \lambda \mathbf{r}' = (\lambda x', \lambda y', \lambda z') \]

to arrive at

\[ \left[ - \frac{\hbar^2}{2 m_\mathrm{e} \lambda^2} {\nabla'}^2 - \frac{e^2}{4\pi\varepsilon_0 \lambda r'} \right] \psi(\mathbf{r}') = E \psi(\mathbf{r}') \]

Choose \(\lambda\) so that

\[ \frac{\hbar^2}{m_\mathrm{e} \lambda^2} = \frac{e^2}{4\pi\varepsilon_0 \lambda} \equiv E_h \]

with the solution

\[ \lambda = \frac{\hbar^2 4\pi\varepsilon_0}{m_\mathrm{e} e^2} \equiv a_0; \qquad E_h = \frac{m_\mathrm{e} e^4}{(4\pi\varepsilon_0)^2 \hbar^2} \]

With \(E' = E/E_h\), we get

\[ \left[ - \frac{1}{2} {\nabla'}^2 - \frac{1}{r'} \right] \psi(\mathbf{r}') = E' \psi(\mathbf{r}') \]

with a solution for the ground state energy that is equal to \(E' = -0.5\) a.u. (or Hartree). The defined quantity \(a_0\) is equal to the Bohr radius and the atomic unit of length is therefore also referred to as Bohr.

Table: Atomic unit conversion factors.

Quantity	Symbol	Atomic unit	SI equivalent
Energy	\(E\)	1 \(E_\mathrm{h}\)	4.359 744\(\times 10^{-18}\) J
Reduced Planck constant	\(h = 2\pi\hbar\)	1 \(\hbar\)	1.054 572\(\times 10^{-34}\) J s
Time	\(t\)	1 \(\hbar E_\mathrm{h}^{-1}\)	2.418 884\(\times 10^{-17}\) s
Length	\(l\)	1 \(a_0\)	5.291 772\(\times 10^{-11}\) m
Speed of light	\(c\)	137.036 \(a_0 E_h \hbar^{-1}\)	2.997 925\(\times 10^{8}\) m s\(^{-1}\)
Electric constant	\(\varepsilon_0\)	1 \(4\pi\varepsilon_0\)	8.854 188\(\times 10^{-12}\) F m\(^{-1}\)
Fine structure constant	\(\alpha\)	1/137.036 \(e^2( a_0 E_h 4\pi\varepsilon_0)^{-1}\)	7.297 353\(\times 10^{3}\)
Charge	\(q\)	1 \(e\)	1.602 176\(\times 10^{-19}\) C
Electric field	\(F\)	1 \(E_h (e a_{0})^{-1}\)	5.142 207\(\times 10^{11}\) V m\(^{-1}\)
Dipole moment	\(\mu\)	1 \(e a_{0}\)	8.478 353\(\times 10^{-30}\) C m
Mass	\(m\)	1 \(m_e\)	9.109 383\(\times 10^{-31}\) kg