Special aspects#
In this section we will discuss a number of issues and questions relating to core spectroscopies, ranging from the physical effect of a core-transition, to technical aspects relating to lowering computational costs. They are ordered by approximate relevance, with some topics being pertient only for certain cases.
Relaxation#
Core spectroscopies exhibit strong relaxation effects, originating in the significant change in shielding of the nuclear charge arising from the creation/annihilation of a core-hole. These effects need to be properly accounted for in order to get good absolute energies, as the lack of this will mean that, e.g. an unrelaxed core-hole system is too high in energy. This explains the previously observed large error obtained using Koopmans’ theorem.
Relaxation of core-ionized systems#
Below we see the effects of relaxation for creating a core-hole in the oxygen/carbon 1s of formaldehyde, illustrated by plotting the total electron density:
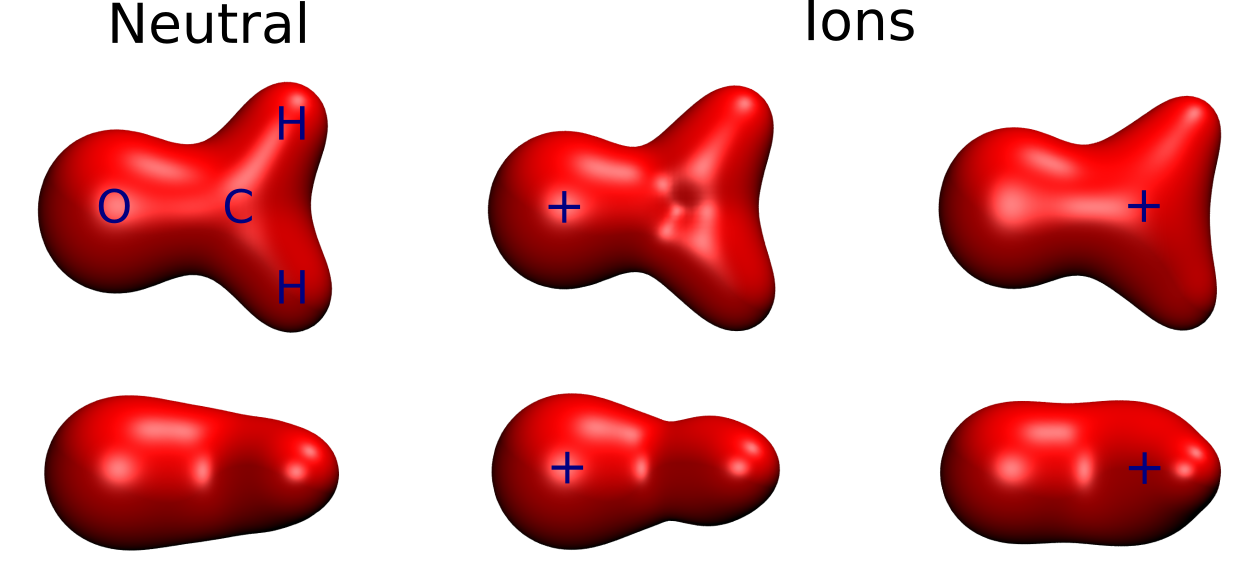
We see that there is a noticable attraction of electron density toward the core-holes, as marked with a +. These effects can be modeled with the \(Z+1\) approximation, within which the change in screening is modeled by substituting the ionized atom with the next element in the periodic table. This can be illustrated with the following radial distribution plots (using cc-pcvdz basis sets, in order to increase flexibility in the core region):
import copy
import adcc
import matplotlib.pyplot as plt
import numpy as np
import veloxchem as vlx
au2ev = 27.211386
Show code cell source
def lorentzian(x, y, xmin, xmax, xstep, gamma):
"""
Lorentzian broadening function
Call: xi,yi = lorentzian(energies, intensities, start energy,
end energy, energy step, gamma)
"""
xi = np.arange(xmin, xmax, xstep)
yi = np.zeros(len(xi))
for i in range(len(xi)):
for k in range(len(x)):
yi[i] = (
yi[i]
+ y[k] * gamma / ((xi[i] - x[k]) ** 2 + (gamma / 2.0) ** 2) / np.pi
)
return xi, yi
water_xyz = """3
O 0.0000000000 0.0000000000 0.1178336003
H -0.7595754146 -0.0000000000 -0.4713344012
H 0.7595754146 0.0000000000 -0.4713344012
"""
water_fluorine_xyz = """3
F 0.0000000000 0.0000000000 0.1178336003
H -0.7595754146 -0.0000000000 -0.4713344012
H 0.7595754146 0.0000000000 -0.4713344012
"""
3Dmol.js failed to load for some reason. Please check your browser console for error messages.
molecule = vlx.Molecule.read_xyz_string(water_xyz)
basis = vlx.MolecularBasis.read(molecule, "CC-PCVDZ")
# Perform SCF calculation
scf_gs = vlx.ScfRestrictedDriver()
gs_results = scf_gs.compute(molecule, basis)
molecule.set_charge(1)
molecule.set_multiplicity(2)
scf_ion = vlx.ScfUnrestrictedDriver()
#Create list of occupied orbitals
occa = list(range(5))
occb = list(range(1, 5))
scf_ion.maximum_overlap(molecule, basis, scf_gs.mol_orbs, occa, occb)
ion_results = scf_ion.compute(molecule, basis)
molecule_F = vlx.Molecule.read_xyz_string(water_fluorine_xyz)
molecule_F.set_charge(1)
basis_F = vlx.MolecularBasis.read(molecule_F, "CC-PCVDZ")
scf_F = vlx.ScfRestrictedDriver()
F_results = scf_F.compute(molecule_F, basis_F)
def get_rho(coords, mo1, mo2, mo3):
r, rho1, rho2, rho3 = [], [], [], []
for i in np.arange(len(coords)):
r.append(coords[i, 0])
rho1.append(coords[i, 0] ** 2 * mo1[i] ** 2)
rho2.append(coords[i, 0] ** 2 * mo2[i] ** 2)
rho3.append(coords[i, 0] ** 2 * mo3[i] ** 2)
return r, rho1, rho2, rho3
vis_drv = vlx.VisualizationDriver()
Ay = 0.0 # oxygen y-position (in au)
Az = 0.1178336003 / 0.529177249 # oxygen z-position (in au)
# Create coordinate object along x-axis (intersecting with O/F atom)
n = 1000
coords = np.zeros((n, 3))
coords[:, 0] = np.linspace(-4, 4, n) # radial points along the x-axis
coords[:, 2] = Az
mo1_gs = np.array(vis_drv.get_mo(coords, molecule, basis, scf_gs.mol_orbs, 0, "alpha"))
mo1_ion = np.array(vis_drv.get_mo(coords, molecule, basis, scf_ion.mol_orbs, 0, "alpha"))
mo1_Z1 = np.array(vis_drv.get_mo(coords, molecule_F, basis_F, scf_F.mol_orbs, 0, "alpha"))
plt.figure(figsize=(10, 6))
plt.subplot(221)
plt.title(r"MO$_{\alpha 1}$ ($1a_1$)")
r, rho1, rho2, rho3 = get_rho(coords, mo1_gs, mo1_ion, mo1_Z1)
plt.plot(r, rho1)
plt.plot(r, rho2)
plt.plot(r, rho3)
plt.legend(("Ground-state", "Core-hole", "Ground-state [Z+1]"))
plt.xlim((0, 0.75))
plt.xlabel("Radius [a.u.]")
plt.ylabel(r"Density [$r^2 \rho$]")
mo2_gs = np.array(vis_drv.get_mo(coords, molecule, basis, scf_gs.mol_orbs, 1, "alpha"))
mo2_ion = np.array(vis_drv.get_mo(coords, molecule, basis, scf_ion.mol_orbs, 1, "alpha"))
mo2_Z1 = np.array(vis_drv.get_mo(coords, molecule_F, basis_F, scf_F.mol_orbs, 1, "alpha"))
plt.subplot(222)
plt.title(r"MO$_{\alpha 2}$ ($2a_1$)")
r, rho1, rho2, rho3 = get_rho(coords, mo2_gs, mo2_ion, mo2_Z1)
plt.plot(r, rho1)
plt.plot(r, rho2)
plt.plot(r, rho3)
plt.xlim((0, 2.5))
plt.xlabel("Radius [a.u.]")
plt.ylabel(r"Density [$r^2 \rho$]")
mo2b_gs = np.array(vis_drv.get_mo(coords, molecule, basis, scf_gs.mol_orbs, 1, "beta"))
mo2b_ion = np.array(vis_drv.get_mo(coords, molecule, basis, scf_ion.mol_orbs, 0, "beta"))
mo2b_Z1 = np.array(vis_drv.get_mo(coords, molecule_F, basis_F, scf_F.mol_orbs, 1, "beta"))
plt.subplot(224)
plt.title(r"MO$_{\beta 2}$ ($2a_1$)")
r, rho1, rho2, rho3 = get_rho(coords, mo2b_gs, mo2b_ion, mo2b_Z1)
plt.plot(r, rho1)
plt.plot(r, rho2)
plt.plot(r, rho3)
plt.xlim((0, 2.5))
plt.xlabel("Radius [a.u.]")
plt.ylabel(r"Density [$r^2 \rho$]")
plt.tight_layout()
plt.show()
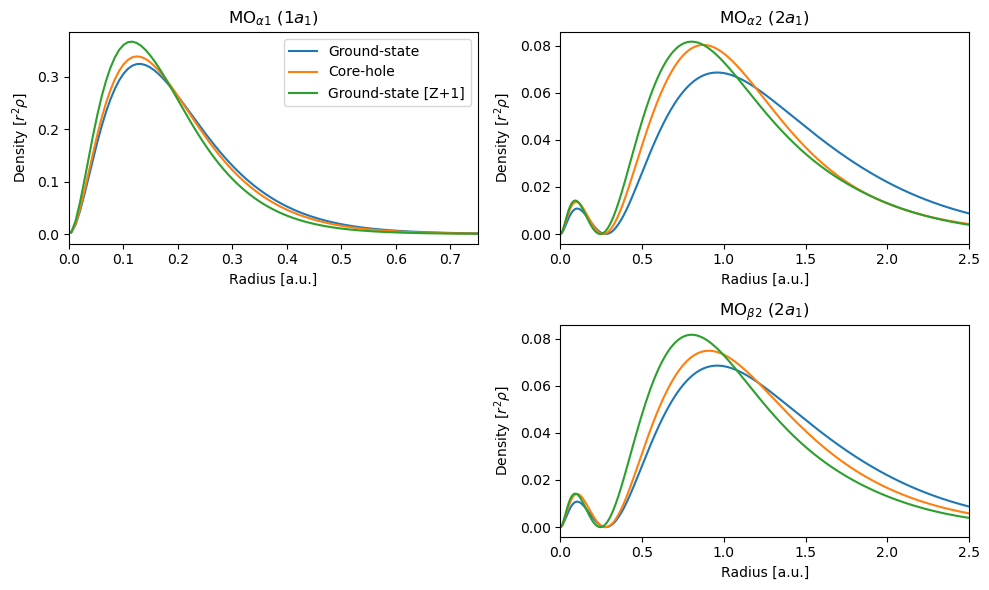
As can be seen, the radial distribution of particularly \(\alpha_2\) for the core-ionized system is closer to \(Z+1\) than to the neutral state, while for \(\alpha_1\) and \(\beta_2\) it is closer to that of the ground state. Also note the differences in the x-scales, with \(\alpha_1\) being more compressed and thus having a larger peak max.
Relaxation of core-(de)excitation#
For X-ray absorption and emission spectroscopy the influence of the relaxation is more complex, on account of the interaction with the created singly-occupied state. Comparing the two spectroscopies, the relaxation processes are partially inverse to each other, with
Relaxation in XAS leading to a more contracted final state, which lowers absorption energies
Relaxation in XES leading to a more decontracted final state, which increases emission energies
In addition to these strong changes in shielding, there are also additional couplings due to the population of a previous unoccupied state (XAS) or the creation of a valence-hole (XES). These effects are smaller and partially counteract the stronger change in shielding from the occupied/unoccupied core orbital, leading to a total picture as follows. Here we illustrate the relaxation effects involved in X-ray absorption (left) and emission (right) spectroscopies. Showing which orbitals primarily contribute to the respective effects, as well as the result in MO energies (or electron densities).:
We here see the four main effects:
X-ray absorption spectroscopy
A strong relaxation effect due to the creation of a core-hole, which leads to the contraction of electron density and scales with element
A weak polarization effect due to coupling with the newly occupied valence state, which partially decontracts the outer valence density and does not scale appreciably with the element
X-ray emission spectroscopy
A strong repulsion effect due to the annihilation of a core-hole, which leads to decontraction of electron density and scales with element
A weaker outer relaxation effect due to the creation of a valence-hole, which leads to contraction of the (outer) valence density and scales with element
These effects balances in different manners, and the exact strength depends heavily on the element and which edge is being probed. As such, the accuracy of a particular method depends on which spectroscopy, element, and edge is considered.
Including relaxation with \(\Delta\)SCF methods#
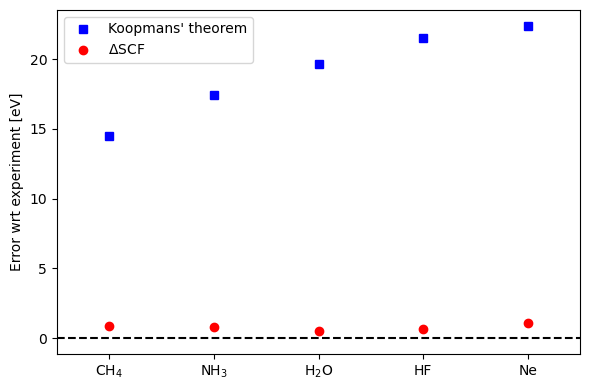
\(\Delta\)SCF methods provide the most direct way of including relaxation, as the core-hole state is explicitly optimized. However, these approaches need to consider each transition explicitly, and will have difficulties in calculating intensities and in properly converging higher excited states. As such, they are mainly useful for considering ionization energies and for providing a reference state for XES calculations. Comparing the performance of calculating IEs of the ten-electron series using Koopmans’ theorem and \(\Delta\)SCF:
methane_mol_str = """
C 0.0000000000 0.0000000000 0.0000000000
H 0.6265918120 0.6265918120 0.6265918120
H -0.6265918120 -0.6265918120 0.6265918120
H -0.6265918120 0.6265918120 -0.6265918120
H 0.6265918120 -0.6265918120 -0.6265918120
"""
ammonia_mol_str = """
N 0.0000000000 0.0000000000 0.1175868000
H 0.9323800000 0.0000000000 -0.2743692000
H -0.4661900000 -0.8074647660 -0.2743692000
H -0.4661900000 0.8074647660 -0.2743692000
"""
water_mol_str = """
O 0.0000000000 0.0000000000 0.1178336003
H -0.7595754146 -0.0000000000 -0.4713344012
H 0.7595754146 0.0000000000 -0.4713344012
"""
hydrofluoride_mol_str = """
H 0.0000000000 0.0000000000 -0.8261856000
F 0.0000000000 0.0000000000 0.0917984000
"""
neon_mol_str = """
Ne 0.0000000000 0.0000000000 0.0000000000
"""
def Koopman_vs_delta(mol_str, basis_label):
molecule = vlx.Molecule.read_molecule_string(mol_str)
basis = vlx.MolecularBasis.read(molecule, basis_label)
# Perform SCF calculation
scf_gs = vlx.ScfRestrictedDriver()
gs_results = scf_gs.compute(molecule, basis)
orbital_energies = gs_results["E_alpha"]
molecule.set_charge(1)
molecule.set_multiplicity(2)
scf_ion = vlx.ScfUnrestrictedDriver()
#Create list of occupied orbitals
nOcc = molecule.number_of_alpha_electrons()
occa = list(range(nOcc))
occb = list(range(1, nOcc))
scf_ion.maximum_overlap(molecule, basis, scf_gs.mol_orbs, occa, occb)
ion_results = scf_ion.compute(molecule, basis)
# Return MO energy and deltaSCF
return -au2ev * orbital_energies[0], au2ev * (
scf_ion.get_scf_energy() - scf_gs.get_scf_energy()
)
# Basis set and container for errors
basis = "cc-pcvdz"
err_koopman, err_delta = [], []
expt, rel = 290.76, 0.11 # experimental IE and scalar-relativistic effects
E_Koopman, E_delta = Koopman_vs_delta(methane_mol_str, basis)
err_koopman.append(E_Koopman + rel - expt)
err_delta.append(E_delta + rel - expt)
expt, rel = 405.52, 0.21 # experimental IE and scalar-relativistic effects
E_Koopman, E_delta = Koopman_vs_delta(ammonia_mol_str, basis)
err_koopman.append(E_Koopman + rel - expt)
err_delta.append(E_delta + rel - expt)
expt, rel = 539.90, 0.37 # experimental IE and scalar-relativistic effects
E_Koopman, E_delta = Koopman_vs_delta(water_mol_str, basis)
err_koopman.append(E_Koopman + rel - expt)
err_delta.append(E_delta + rel - expt)
expt, rel = 694.10, 0.61 # experimental IE and scalar-relativistic effects
E_Koopman, E_delta = Koopman_vs_delta(hydrofluoride_mol_str, basis)
err_koopman.append(E_Koopman + rel - expt)
err_delta.append(E_delta + rel - expt)
expt, rel = 870.09, 0.94 # experimental IE and scalar-relativistic effects
E_Koopman, E_delta = Koopman_vs_delta(neon_mol_str, basis)
err_koopman.append(E_Koopman + rel - expt)
err_delta.append(E_delta + rel - expt)
Show code cell output
* Info * Reading basis set from file: /home/emi/miniconda3/envs/echem/lib/python3.11/site-packages/veloxchem/basis/CC-PCVDZ
Molecular Basis (Atomic Basis)
================================
Basis: CC-PCVDZ
Atom Contracted GTOs Primitive GTOs
H (2S,1P) (4S,1P)
C (4S,3P,1D) (18S,5P,1D)
Contracted Basis Functions : 38
Primitive Basis Functions : 66
Self Consistent Field Driver Setup
====================================
Wave Function Model : Spin-Restricted Hartree-Fock
Initial Guess Model : Superposition of Atomic Densities
Convergence Accelerator : Two Level Direct Inversion of Iterative Subspace
Max. Number of Iterations : 50
Max. Number of Error Vectors : 10
Convergence Threshold : 1.0e-06
ERI Screening Scheme : Cauchy Schwarz + Density
ERI Screening Mode : Dynamic
ERI Screening Threshold : 1.0e-12
Linear Dependence Threshold : 1.0e-06
* Info * Nuclear repulsion energy: 13.4937111288 a.u.
* Info * Overlap matrix computed in 0.00 sec.
* Info * Kinetic energy matrix computed in 0.00 sec.
* Info * Nuclear potential matrix computed in 0.00 sec.
* Info * Orthogonalization matrix computed in 0.00 sec.
* Info * SAD initial guess computed in 0.00 sec.
* Info * Starting Reduced Basis SCF calculation...
* Info * ...done. SCF energy in reduced basis set: -40.176641252708 a.u. Time: 0.08 sec.
* Info * Overlap matrix computed in 0.00 sec.
* Info * Kinetic energy matrix computed in 0.00 sec.
* Info * Nuclear potential matrix computed in 0.00 sec.
* Info * Orthogonalization matrix computed in 0.00 sec.
Iter. | Hartree-Fock Energy | Energy Change | Gradient Norm | Max. Gradient | Density Change
--------------------------------------------------------------------------------------------
1 -40.198632549790 0.0000000000 0.07238664 0.00936881 0.00000000
2 -40.199216137990 -0.0005835882 0.00782091 0.00097082 0.02494254
3 -40.199223311012 -0.0000071730 0.00284629 0.00037349 0.00277747
4 -40.199224544997 -0.0000012340 0.00033787 0.00005236 0.00101091
5 -40.199224580341 -0.0000000353 0.00002279 0.00000407 0.00032567
6 -40.199224580473 -0.0000000001 0.00000241 0.00000058 0.00002005
7 -40.199224580475 -0.0000000000 0.00000024 0.00000006 0.00000128
*** SCF converged in 7 iterations. Time: 0.45 sec.
Spin-Restricted Hartree-Fock:
-----------------------------
Total Energy : -40.1992245805 a.u.
Electronic Energy : -53.6929357092 a.u.
Nuclear Repulsion Energy : 13.4937111288 a.u.
------------------------------------
Gradient Norm : 0.0000002419 a.u.
Ground State Information
------------------------
Charge of Molecule : 0.0
Multiplicity (2S+1) : 1.0
Magnetic Quantum Number (M_S) : 0.0
Spin Restricted Orbitals
------------------------
Molecular Orbital No. 1:
--------------------------
Occupation: 2.000 Energy: -11.21468 a.u.
( 1 C 1s : 1.00)
Molecular Orbital No. 2:
--------------------------
Occupation: 2.000 Energy: -0.94394 a.u.
( 1 C 2s : 0.36) ( 1 C 3s : 0.24) ( 2 H 1s : 0.19)
( 3 H 1s : 0.19) ( 4 H 1s : 0.19) ( 5 H 1s : 0.19)
Molecular Orbital No. 3:
--------------------------
Occupation: 2.000 Energy: -0.54399 a.u.
( 1 C 1p+1: 0.27) ( 1 C 1p-1: -0.24) ( 1 C 1p0 : -0.22)
( 4 H 1s : -0.15) ( 5 H 1s : 0.39) ( 5 H 2s : 0.16)
Molecular Orbital No. 4:
--------------------------
Occupation: 2.000 Energy: -0.54399 a.u.
( 1 C 1p+1: 0.22) ( 1 C 1p-1: 0.35) ( 1 C 2p-1: 0.16)
( 2 H 1s : 0.25) ( 3 H 1s : -0.36)
Molecular Orbital No. 5:
--------------------------
Occupation: 2.000 Energy: -0.54399 a.u.
( 1 C 1p+1: 0.24) ( 1 C 1p0 : 0.35) ( 1 C 2p0 : 0.16)
( 2 H 1s : 0.29) ( 4 H 1s : -0.34)
Molecular Orbital No. 6:
--------------------------
Occupation: 0.000 Energy: 0.19200 a.u.
( 1 C 3s : 2.43) ( 2 H 2s : -0.86) ( 3 H 2s : -0.86)
( 4 H 2s : -0.86) ( 5 H 2s : -0.86)
Molecular Orbital No. 7:
--------------------------
Occupation: 0.000 Energy: 0.27467 a.u.
( 1 C 1p0 : -0.27) ( 1 C 2p+1: -0.40) ( 1 C 2p-1: 0.35)
( 1 C 2p0 : -1.32) ( 2 H 2s : 1.27) ( 3 H 2s : 1.17)
( 4 H 2s : -1.92) ( 5 H 2s : -0.52)
Molecular Orbital No. 8:
--------------------------
Occupation: 0.000 Energy: 0.27467 a.u.
( 1 C 1p+1: -0.23) ( 1 C 2p+1: -1.11) ( 1 C 2p-1: 0.71)
( 1 C 2p0 : 0.53) ( 3 H 2s : -0.86) ( 4 H 2s : -1.20)
( 5 H 2s : 2.18)
Molecular Orbital No. 9:
--------------------------
Occupation: 0.000 Energy: 0.27467 a.u.
( 1 C 1p+1: 0.16) ( 1 C 1p-1: 0.25) ( 1 C 2p+1: 0.79)
( 1 C 2p-1: 1.18) ( 2 H 2s : -1.89) ( 3 H 2s : 1.76)
( 4 H 2s : -0.30) ( 5 H 2s : 0.43)
Molecular Orbital No. 10:
--------------------------
Occupation: 0.000 Energy: 0.58864 a.u.
( 1 C 1p+1: -0.16) ( 1 C 1p0 : 0.24) ( 1 C 2p+1: 0.64)
( 1 C 2p-1: -0.41) ( 1 C 2p0 : -0.96) ( 2 H 1s : 0.28)
( 3 H 1s : 0.47) ( 5 H 1s : -0.78)
Ground State Dipole Moment
----------------------------
X : -0.000000 a.u. -0.000000 Debye
Y : 0.000000 a.u. 0.000000 Debye
Z : 0.000000 a.u. 0.000000 Debye
Total : 0.000000 a.u. 0.000000 Debye
* Info * Checkpoint written to file: vlx_20240912_25ae728a.scf.h5
Self Consistent Field Driver Setup
====================================
Wave Function Model : Spin-Unrestricted Hartree-Fock
Initial Guess Model : Restart from Checkpoint
Convergence Accelerator : Direct Inversion of Iterative Subspace
Max. Number of Iterations : 50
Max. Number of Error Vectors : 10
Convergence Threshold : 1.0e-06
ERI Screening Scheme : Cauchy Schwarz + Density
ERI Screening Mode : Dynamic
ERI Screening Threshold : 1.0e-12
Linear Dependence Threshold : 1.0e-06
* Info * Nuclear repulsion energy: 13.4937111288 a.u.
* Info * Overlap matrix computed in 0.00 sec.
* Info * Kinetic energy matrix computed in 0.00 sec.
* Info * Nuclear potential matrix computed in 0.00 sec.
* Info * Orthogonalization matrix computed in 0.00 sec.
* Info * Restarting from checkpoint file: vlx_20240912_25ae728a.scf.h5
Iter. | Hartree-Fock Energy | Energy Change | Gradient Norm | Max. Gradient | Density Change
--------------------------------------------------------------------------------------------
1 -28.984548233126 0.0000000000 2.72929056 0.75211056 0.00000000
2 -29.383245222949 -0.3986969898 1.03746343 0.14598216 0.84846701
3 -29.480740305899 -0.0974950829 0.17120996 0.02756281 0.34603159
4 -29.484157355961 -0.0034170501 0.03303526 0.00415502 0.06446845
5 -29.484720018471 -0.0005626625 0.01405409 0.00155239 0.02807396
6 -29.484843881109 -0.0001238626 0.00254185 0.00037454 0.01842700
7 -29.484845836451 -0.0000019553 0.00046743 0.00007484 0.00338992
8 -29.484845893262 -0.0000000568 0.00008456 0.00001002 0.00035811
9 -29.484845895285 -0.0000000020 0.00001190 0.00000162 0.00007186
10 -29.484845895330 -0.0000000000 0.00000170 0.00000025 0.00001234
11 -29.484845895330 -0.0000000000 0.00000013 0.00000002 0.00000111
* Info * Checkpoint written to file: vlx_20240912_25ae728a.scf.h5
* Info * SCF results written to file: vlx_20240912_25ae728a.scf.results.h5
*** SCF converged in 11 iterations. Time: 0.62 sec.
Spin-Unrestricted Hartree-Fock:
-------------------------------
Total Energy : -29.4848458953 a.u.
Electronic Energy : -42.9785570241 a.u.
Nuclear Repulsion Energy : 13.4937111288 a.u.
------------------------------------
Gradient Norm : 0.0000001275 a.u.
Ground State Information
------------------------
Charge of Molecule : 1.0
Magnetic Quantum Number (M_S) : 0.5
Expectation value of S**2 : 0.7756
Spin Unrestricted Alpha Orbitals
--------------------------------
Molecular Orbital No. 1:
--------------------------
Occupation: 1.000 Energy: -13.84796 a.u.
( 1 C 1s : 1.07)
Molecular Orbital No. 2:
--------------------------
Occupation: 1.000 Energy: -1.45098 a.u.
( 1 C 2s : 0.61)
Molecular Orbital No. 3:
--------------------------
Occupation: 1.000 Energy: -0.99657 a.u.
( 1 C 1p+1: -0.28) ( 1 C 1p0 : -0.60) ( 2 H 1s : -0.24)
( 4 H 1s : 0.19)
Molecular Orbital No. 4:
--------------------------
Occupation: 1.000 Energy: -0.99657 a.u.
( 1 C 1p+1: 0.29) ( 1 C 1p-1: 0.55) ( 1 C 1p0 : -0.24)
( 3 H 1s : -0.26)
Molecular Orbital No. 5:
--------------------------
Occupation: 1.000 Energy: -0.99657 a.u.
( 1 C 1p+1: 0.53) ( 1 C 1p-1: -0.36) ( 1 C 1p0 : -0.18)
( 4 H 1s : -0.17) ( 5 H 1s : 0.26)
Molecular Orbital No. 6:
--------------------------
Occupation: 0.000 Energy: -0.09031 a.u.
( 1 C 2s : 0.26) ( 1 C 3s : 1.85) ( 2 H 2s : -0.74)
( 3 H 2s : -0.74) ( 4 H 2s : -0.74) ( 5 H 2s : -0.74)
Molecular Orbital No. 7:
--------------------------
Occupation: 0.000 Energy: -0.02311 a.u.
( 1 C 1p+1: -0.36) ( 1 C 1p0 : -0.20) ( 1 C 2p+1: -0.81)
( 1 C 2p-1: 0.23) ( 1 C 2p0 : -0.46) ( 2 H 2s : 1.17)
( 4 H 1s : -0.18) ( 4 H 2s : -1.70) ( 5 H 2s : 0.67)
Molecular Orbital No. 8:
--------------------------
Occupation: 0.000 Energy: -0.02311 a.u.
( 1 C 1p+1: -0.22) ( 1 C 1p-1: -0.27) ( 1 C 1p0 : 0.26)
( 1 C 2p+1: -0.49) ( 1 C 2p-1: -0.60) ( 1 C 2p0 : 0.57)
( 2 H 2s : 0.58) ( 3 H 1s : -0.20) ( 3 H 2s : -1.88)
( 4 H 2s : 0.76) ( 5 H 2s : 0.53)
Molecular Orbital No. 9:
--------------------------
Occupation: 0.000 Energy: -0.02311 a.u.
( 1 C 1p-1: 0.32) ( 1 C 1p0 : 0.28) ( 1 C 2p-1: 0.72)
( 1 C 2p0 : 0.62) ( 2 H 2s : -1.36) ( 4 H 2s : -0.27)
( 5 H 1s : 0.18) ( 5 H 2s : 1.68)
Molecular Orbital No. 10:
--------------------------
Occupation: 0.000 Energy: 0.27795 a.u.
( 1 C 1p+1: -0.24) ( 1 C 1p0 : 0.33) ( 1 C 2p+1: 0.89)
( 1 C 2p-1: 0.35) ( 1 C 2p0 : -1.24) ( 3 H 1s : 0.61)
( 3 H 2s : 0.38) ( 4 H 1s : -0.17) ( 5 H 1s : -0.44)
( 5 H 2s : -0.27)
Spin Unrestricted Beta Orbitals
-------------------------------
Molecular Orbital No. 1:
--------------------------
Occupation: 1.000 Energy: -1.36903 a.u.
( 1 C 2s : 0.49) ( 1 C 3s : 0.19) ( 2 H 1s : 0.17)
( 3 H 1s : 0.17) ( 4 H 1s : 0.17) ( 5 H 1s : 0.17)
Molecular Orbital No. 2:
--------------------------
Occupation: 1.000 Energy: -0.96052 a.u.
( 1 C 1p+1: -0.18) ( 1 C 1p-1: 0.19) ( 1 C 1p0 : -0.52)
( 2 H 1s : -0.17) ( 3 H 1s : -0.18) ( 4 H 1s : 0.30)
Molecular Orbital No. 3:
--------------------------
Occupation: 1.000 Energy: -0.96052 a.u.
( 1 C 1p+1: 0.51) ( 1 C 1p-1: 0.28) ( 2 H 1s : 0.24)
( 3 H 1s : -0.29)
Molecular Orbital No. 4:
--------------------------
Occupation: 1.000 Energy: -0.96052 a.u.
( 1 C 1p+1: -0.22) ( 1 C 1p-1: 0.48) ( 1 C 1p0 : 0.25)
( 2 H 1s : 0.17) ( 4 H 1s : 0.15) ( 5 H 1s : -0.32)
Molecular Orbital No. 5:
--------------------------
Occupation: 0.000 Energy: -10.19964 a.u.
( 1 C 1s : 1.00)
Molecular Orbital No. 6:
--------------------------
Occupation: 0.000 Energy: -0.07555 a.u.
( 1 C 2s : 0.20) ( 1 C 3s : 2.03) ( 2 H 2s : -0.78)
( 3 H 2s : -0.78) ( 4 H 2s : -0.78) ( 5 H 2s : -0.78)
Molecular Orbital No. 7:
--------------------------
Occupation: 0.000 Energy: -0.01250 a.u.
( 1 C 1p-1: 0.17) ( 1 C 1p0 : -0.37) ( 1 C 2p+1: -0.16)
( 1 C 2p-1: 0.46) ( 1 C 2p0 : -0.98) ( 2 H 2s : 0.71)
( 3 H 2s : 1.32) ( 4 H 1s : -0.16) ( 4 H 2s : -1.66)
( 5 H 2s : -0.37)
Molecular Orbital No. 8:
--------------------------
Occupation: 0.000 Energy: -0.01250 a.u.
( 1 C 1p-1: 0.34) ( 1 C 1p0 : 0.18) ( 1 C 2p+1: -0.34)
( 1 C 2p-1: 0.92) ( 1 C 2p0 : 0.49) ( 2 H 2s : -1.11)
( 4 H 2s : -0.80) ( 5 H 1s : 0.17) ( 5 H 2s : 1.81)
Molecular Orbital No. 9:
--------------------------
Occupation: 0.000 Energy: -0.01250 a.u.
( 1 C 1p+1: 0.38) ( 1 C 2p+1: 1.02) ( 1 C 2p-1: 0.38)
( 2 H 2s : -1.46) ( 3 H 2s : 1.45) ( 4 H 2s : 0.68)
( 5 H 2s : -0.67)
Ground State Dipole Moment
----------------------------
*** Warning: Molecule has non-zero charge. Dipole
moment will be dependent on the choice of origin.
Center of nuclear charge is chosen as the origin.
X : -0.000000 a.u. -0.000000 Debye
Y : 0.000000 a.u. 0.000000 Debye
Z : 0.000000 a.u. 0.000000 Debye
Total : 0.000000 a.u. 0.000000 Debye
* Info * Reading basis set from file: /home/emi/miniconda3/envs/echem/lib/python3.11/site-packages/veloxchem/basis/CC-PCVDZ
Molecular Basis (Atomic Basis)
================================
Basis: CC-PCVDZ
Atom Contracted GTOs Primitive GTOs
H (2S,1P) (4S,1P)
N (4S,3P,1D) (18S,5P,1D)
Contracted Basis Functions : 33
Primitive Basis Functions : 59
Self Consistent Field Driver Setup
====================================
Wave Function Model : Spin-Restricted Hartree-Fock
Initial Guess Model : Superposition of Atomic Densities
Convergence Accelerator : Two Level Direct Inversion of Iterative Subspace
Max. Number of Iterations : 50
Max. Number of Error Vectors : 10
Convergence Threshold : 1.0e-06
ERI Screening Scheme : Cauchy Schwarz + Density
ERI Screening Mode : Dynamic
ERI Screening Threshold : 1.0e-12
Linear Dependence Threshold : 1.0e-06
* Info * Nuclear repulsion energy: 11.9703270415 a.u.
* Info * Overlap matrix computed in 0.00 sec.
* Info * Kinetic energy matrix computed in 0.00 sec.
* Info * Nuclear potential matrix computed in 0.00 sec.
* Info * Orthogonalization matrix computed in 0.00 sec.
* Info * SAD initial guess computed in 0.00 sec.
* Info * Starting Reduced Basis SCF calculation...
* Info * ...done. SCF energy in reduced basis set: -56.154702188708 a.u. Time: 0.06 sec.
* Info * Overlap matrix computed in 0.00 sec.
* Info * Kinetic energy matrix computed in 0.00 sec.
* Info * Nuclear potential matrix computed in 0.00 sec.
* Info * Orthogonalization matrix computed in 0.00 sec.
Iter. | Hartree-Fock Energy | Energy Change | Gradient Norm | Max. Gradient | Density Change
--------------------------------------------------------------------------------------------
1 -56.195358785586 0.0000000000 0.09236701 0.01092262 0.00000000
2 -56.196206735532 -0.0008479499 0.01551902 0.00289180 0.03204290
3 -56.196232682551 -0.0000259470 0.00329250 0.00061368 0.00416037
4 -56.196236230580 -0.0000035480 0.00129802 0.00014764 0.00241244
5 -56.196236654350 -0.0000004238 0.00047049 0.00009292 0.00079374
6 -56.196236728370 -0.0000000740 0.00006997 0.00001054 0.00047731
7 -56.196236729650 -0.0000000013 0.00000421 0.00000053 0.00006073
8 -56.196236729653 -0.0000000000 0.00000048 0.00000006 0.00000255
*** SCF converged in 8 iterations. Time: 0.48 sec.
Spin-Restricted Hartree-Fock:
-----------------------------
Total Energy : -56.1962367297 a.u.
Electronic Energy : -68.1665637711 a.u.
Nuclear Repulsion Energy : 11.9703270415 a.u.
------------------------------------
Gradient Norm : 0.0000004806 a.u.
Ground State Information
------------------------
Charge of Molecule : 0.0
Multiplicity (2S+1) : 1.0
Magnetic Quantum Number (M_S) : 0.0
Spin Restricted Orbitals
------------------------
Molecular Orbital No. 1:
--------------------------
Occupation: 2.000 Energy: -15.53583 a.u.
( 1 N 1s : -1.00)
Molecular Orbital No. 2:
--------------------------
Occupation: 2.000 Energy: -1.13384 a.u.
( 1 N 2s : 0.40) ( 1 N 3s : 0.28) ( 2 H 1s : 0.20)
( 3 H 1s : 0.20) ( 4 H 1s : 0.20)
Molecular Orbital No. 3:
--------------------------
Occupation: 2.000 Energy: -0.61616 a.u.
( 1 N 1p-1: -0.45) ( 1 N 2p-1: -0.21) ( 3 H 1s : 0.32)
( 4 H 1s : -0.32)
Molecular Orbital No. 4:
--------------------------
Occupation: 2.000 Energy: -0.61616 a.u.
( 1 N 1p+1: 0.45) ( 1 N 2p+1: 0.21) ( 2 H 1s : 0.37)
( 3 H 1s : -0.19) ( 4 H 1s : -0.19)
Molecular Orbital No. 5:
--------------------------
Occupation: 2.000 Energy: -0.42176 a.u.
( 1 N 3s : 0.30) ( 1 N 1p0 : 0.54) ( 1 N 2p0 : 0.46)
Molecular Orbital No. 6:
--------------------------
Occupation: 0.000 Energy: 0.18607 a.u.
( 1 N 3s : 1.50) ( 1 N 2p0 : -0.34) ( 2 H 2s : -0.74)
( 3 H 2s : -0.74) ( 4 H 2s : -0.74)
Molecular Orbital No. 7:
--------------------------
Occupation: 0.000 Energy: 0.27050 a.u.
( 1 N 1p-1: -0.29) ( 1 N 2p-1: -0.90) ( 3 H 2s : -1.56)
( 4 H 2s : 1.56)
Molecular Orbital No. 8:
--------------------------
Occupation: 0.000 Energy: 0.27050 a.u.
( 1 N 1p+1: -0.29) ( 1 N 2p+1: -0.90) ( 2 H 2s : 1.80)
( 3 H 2s : -0.90) ( 4 H 2s : -0.90)
Molecular Orbital No. 9:
--------------------------
Occupation: 0.000 Energy: 0.72999 a.u.
( 1 N 2p+1: -0.68) ( 2 H 1s : 1.01) ( 2 H 2s : -0.54)
( 3 H 1s : -0.51) ( 3 H 2s : 0.27) ( 4 H 1s : -0.51)
( 4 H 2s : 0.27)
Molecular Orbital No. 10:
--------------------------
Occupation: 0.000 Energy: 0.72999 a.u.
( 1 N 2p-1: -0.68) ( 3 H 1s : -0.88) ( 3 H 2s : 0.47)
( 4 H 1s : 0.88) ( 4 H 2s : -0.47)
Ground State Dipole Moment
----------------------------
X : 0.000000 a.u. 0.000000 Debye
Y : 0.000000 a.u. 0.000000 Debye
Z : -0.681083 a.u. -1.731140 Debye
Total : 0.681083 a.u. 1.731140 Debye
* Info * Checkpoint written to file: vlx_20240912_86e55696.scf.h5
Self Consistent Field Driver Setup
====================================
Wave Function Model : Spin-Unrestricted Hartree-Fock
Initial Guess Model : Restart from Checkpoint
Convergence Accelerator : Direct Inversion of Iterative Subspace
Max. Number of Iterations : 50
Max. Number of Error Vectors : 10
Convergence Threshold : 1.0e-06
ERI Screening Scheme : Cauchy Schwarz + Density
ERI Screening Mode : Dynamic
ERI Screening Threshold : 1.0e-12
Linear Dependence Threshold : 1.0e-06
* Info * Nuclear repulsion energy: 11.9703270415 a.u.
* Info * Overlap matrix computed in 0.00 sec.
* Info * Kinetic energy matrix computed in 0.00 sec.
* Info * Nuclear potential matrix computed in 0.00 sec.
* Info * Orthogonalization matrix computed in 0.00 sec.
* Info * Restarting from checkpoint file: vlx_20240912_86e55696.scf.h5
Iter. | Hartree-Fock Energy | Energy Change | Gradient Norm | Max. Gradient | Density Change
--------------------------------------------------------------------------------------------
1 -40.660410101572 0.0000000000 3.36296681 0.93787381 0.00000000
2 -41.122191658113 -0.4617815565 1.36758506 0.19392095 0.86529171
3 -41.266669310780 -0.1444776527 0.21528914 0.02793667 0.35551128
4 -41.271020414678 -0.0043511039 0.03449561 0.00531354 0.06580037
5 -41.271483608593 -0.0004631939 0.01412355 0.00223336 0.02171266
6 -41.271579300234 -0.0000956916 0.00321463 0.00044586 0.01358060
7 -41.271582780015 -0.0000034798 0.00076046 0.00010369 0.00252762
8 -41.271582946469 -0.0000001665 0.00015419 0.00002015 0.00053815
9 -41.271582952575 -0.0000000061 0.00003472 0.00000430 0.00011550
10 -41.271582952900 -0.0000000003 0.00000726 0.00000138 0.00002156
11 -41.271582952917 -0.0000000000 0.00000201 0.00000041 0.00000518
12 -41.271582952918 -0.0000000000 0.00000036 0.00000006 0.00000170
* Info * Checkpoint written to file: vlx_20240912_86e55696.scf.h5
* Info * SCF results written to file: vlx_20240912_86e55696.scf.results.h5
*** SCF converged in 12 iterations. Time: 0.65 sec.
Spin-Unrestricted Hartree-Fock:
-------------------------------
Total Energy : -41.2715829529 a.u.
Electronic Energy : -53.2419099944 a.u.
Nuclear Repulsion Energy : 11.9703270415 a.u.
------------------------------------
Gradient Norm : 0.0000003577 a.u.
Ground State Information
------------------------
Charge of Molecule : 1.0
Magnetic Quantum Number (M_S) : 0.5
Expectation value of S**2 : 0.7708
Spin Unrestricted Alpha Orbitals
--------------------------------
Molecular Orbital No. 1:
--------------------------
Occupation: 1.000 Energy: -18.57272 a.u.
( 1 N 1s : -1.06)
Molecular Orbital No. 2:
--------------------------
Occupation: 1.000 Energy: -1.71997 a.u.
( 1 N 2s : 0.61) ( 1 N 3s : 0.19) ( 2 H 1s : 0.16)
( 3 H 1s : 0.16) ( 4 H 1s : 0.16)
Molecular Orbital No. 3:
--------------------------
Occupation: 1.000 Energy: -1.14527 a.u.
( 1 N 1p+1: -0.67) ( 1 N 2p+1: -0.17) ( 2 H 1s : -0.28)
Molecular Orbital No. 4:
--------------------------
Occupation: 1.000 Energy: -1.14527 a.u.
( 1 N 1p-1: -0.67) ( 1 N 2p-1: -0.17) ( 3 H 1s : 0.24)
( 4 H 1s : -0.24)
Molecular Orbital No. 5:
--------------------------
Occupation: 1.000 Energy: -1.00217 a.u.
( 1 N 2s : 0.18) ( 1 N 1p0 : 0.75) ( 1 N 2p0 : 0.26)
Molecular Orbital No. 6:
--------------------------
Occupation: 0.000 Energy: -0.13072 a.u.
( 1 N 2s : 0.22) ( 1 N 3s : 1.14) ( 1 N 1p0 : -0.18)
( 1 N 2p0 : -0.20) ( 2 H 2s : -0.64) ( 3 H 2s : -0.64)
( 4 H 2s : -0.64)
Molecular Orbital No. 7:
--------------------------
Occupation: 0.000 Energy: -0.05496 a.u.
( 1 N 1p-1: -0.38) ( 1 N 2p-1: -0.62) ( 3 H 1s : -0.18)
( 3 H 2s : -1.30) ( 4 H 1s : 0.18) ( 4 H 2s : 1.30)
Molecular Orbital No. 8:
--------------------------
Occupation: 0.000 Energy: -0.05496 a.u.
( 1 N 1p+1: -0.38) ( 1 N 2p+1: -0.62) ( 2 H 1s : 0.21)
( 2 H 2s : 1.51) ( 3 H 2s : -0.75) ( 4 H 2s : -0.75)
Molecular Orbital No. 9:
--------------------------
Occupation: 0.000 Energy: 0.38300 a.u.
( 1 N 1p+1: -0.19) ( 1 N 2p+1: -0.29) ( 2 H 1s : 1.00)
( 2 H 2s : -0.93) ( 3 H 1s : -0.50) ( 3 H 2s : 0.47)
( 4 H 1s : -0.50) ( 4 H 2s : 0.47)
Molecular Orbital No. 10:
--------------------------
Occupation: 0.000 Energy: 0.38300 a.u.
( 1 N 1p-1: -0.19) ( 1 N 2p-1: -0.29) ( 3 H 1s : -0.87)
( 3 H 2s : 0.81) ( 4 H 1s : 0.87) ( 4 H 2s : -0.81)
Spin Unrestricted Beta Orbitals
-------------------------------
Molecular Orbital No. 1:
--------------------------
Occupation: 1.000 Energy: -1.62136 a.u.
( 1 N 2s : 0.51) ( 1 N 3s : 0.23) ( 2 H 1s : 0.18)
( 3 H 1s : 0.18) ( 4 H 1s : 0.18)
Molecular Orbital No. 2:
--------------------------
Occupation: 1.000 Energy: -1.09628 a.u.
( 1 N 1p+1: 0.60) ( 1 N 2p+1: 0.18) ( 2 H 1s : 0.33)
( 3 H 1s : -0.16) ( 4 H 1s : -0.16)
Molecular Orbital No. 3:
--------------------------
Occupation: 1.000 Energy: -1.09628 a.u.
( 1 N 1p-1: 0.60) ( 1 N 2p-1: 0.18) ( 3 H 1s : -0.28)
( 4 H 1s : 0.28)
Molecular Orbital No. 4:
--------------------------
Occupation: 1.000 Energy: -0.93070 a.u.
( 1 N 2s : 0.18) ( 1 N 3s : 0.19) ( 1 N 1p0 : 0.70)
( 1 N 2p0 : 0.32)
Molecular Orbital No. 5:
--------------------------
Occupation: 0.000 Energy: -14.30674 a.u.
( 1 N 1s : -1.00)
Molecular Orbital No. 6:
--------------------------
Occupation: 0.000 Energy: -0.11641 a.u.
( 1 N 2s : 0.18) ( 1 N 3s : 1.24) ( 1 N 1p0 : -0.17)
( 1 N 2p0 : -0.22) ( 2 H 2s : -0.67) ( 3 H 2s : -0.67)
( 4 H 2s : -0.67)
Molecular Orbital No. 7:
--------------------------
Occupation: 0.000 Energy: -0.04172 a.u.
( 1 N 1p-1: -0.38) ( 1 N 2p-1: -0.69) ( 3 H 1s : -0.16)
( 3 H 2s : -1.35) ( 4 H 1s : 0.16) ( 4 H 2s : 1.35)
Molecular Orbital No. 8:
--------------------------
Occupation: 0.000 Energy: -0.04172 a.u.
( 1 N 1p+1: -0.38) ( 1 N 2p+1: -0.69) ( 2 H 1s : 0.18)
( 2 H 2s : 1.55) ( 3 H 2s : -0.78) ( 4 H 2s : -0.78)
Molecular Orbital No. 9:
--------------------------
Occupation: 0.000 Energy: 0.37116 a.u.
( 1 N 1p+1: -0.16) ( 1 N 2p+1: -0.40) ( 2 H 1s : 1.00)
( 2 H 2s : -0.85) ( 3 H 1s : -0.50) ( 3 H 2s : 0.43)
( 4 H 1s : -0.50) ( 4 H 2s : 0.43)
Ground State Dipole Moment
----------------------------
*** Warning: Molecule has non-zero charge. Dipole
moment will be dependent on the choice of origin.
Center of nuclear charge is chosen as the origin.
X : -0.000000 a.u. -0.000000 Debye
Y : 0.000000 a.u. 0.000000 Debye
Z : -0.872565 a.u. -2.217840 Debye
Total : 0.872565 a.u. 2.217840 Debye
* Info * Reading basis set from file: /home/emi/miniconda3/envs/echem/lib/python3.11/site-packages/veloxchem/basis/CC-PCVDZ
Molecular Basis (Atomic Basis)
================================
Basis: CC-PCVDZ
Atom Contracted GTOs Primitive GTOs
O (4S,3P,1D) (18S,5P,1D)
H (2S,1P) (4S,1P)
Contracted Basis Functions : 28
Primitive Basis Functions : 52
Self Consistent Field Driver Setup
====================================
Wave Function Model : Spin-Restricted Hartree-Fock
Initial Guess Model : Superposition of Atomic Densities
Convergence Accelerator : Two Level Direct Inversion of Iterative Subspace
Max. Number of Iterations : 50
Max. Number of Error Vectors : 10
Convergence Threshold : 1.0e-06
ERI Screening Scheme : Cauchy Schwarz + Density
ERI Screening Mode : Dynamic
ERI Screening Threshold : 1.0e-12
Linear Dependence Threshold : 1.0e-06
* Info * Nuclear repulsion energy: 9.1561447194 a.u.
* Info * Overlap matrix computed in 0.00 sec.
* Info * Kinetic energy matrix computed in 0.00 sec.
* Info * Nuclear potential matrix computed in 0.00 sec.
* Info * Orthogonalization matrix computed in 0.00 sec.
* Info * SAD initial guess computed in 0.00 sec.
* Info * Starting Reduced Basis SCF calculation...
* Info * ...done. SCF energy in reduced basis set: -75.980954854746 a.u. Time: 0.04 sec.
* Info * Overlap matrix computed in 0.00 sec.
* Info * Kinetic energy matrix computed in 0.00 sec.
* Info * Nuclear potential matrix computed in 0.00 sec.
* Info * Orthogonalization matrix computed in 0.00 sec.
Iter. | Hartree-Fock Energy | Energy Change | Gradient Norm | Max. Gradient | Density Change
--------------------------------------------------------------------------------------------
1 -76.025912394461 0.0000000000 0.10613691 0.01096404 0.00000000
2 -76.026931952439 -0.0010195580 0.02019241 0.00280757 0.02550308
3 -76.026976262238 -0.0000443098 0.00419173 0.00085956 0.00453733
4 -76.026979226222 -0.0000029640 0.00218984 0.00030105 0.00163383
5 -76.026979655187 -0.0000004290 0.00033786 0.00007031 0.00046129
6 -76.026979678134 -0.0000000229 0.00003955 0.00000573 0.00016589
7 -76.026979678489 -0.0000000004 0.00000246 0.00000041 0.00002137
8 -76.026979678490 -0.0000000000 0.00000049 0.00000007 0.00000086
*** SCF converged in 8 iterations. Time: 0.48 sec.
Spin-Restricted Hartree-Fock:
-----------------------------
Total Energy : -76.0269796785 a.u.
Electronic Energy : -85.1831243979 a.u.
Nuclear Repulsion Energy : 9.1561447194 a.u.
------------------------------------
Gradient Norm : 0.0000004877 a.u.
Ground State Information
------------------------
Charge of Molecule : 0.0
Multiplicity (2S+1) : 1.0
Magnetic Quantum Number (M_S) : 0.0
Spin Restricted Orbitals
------------------------
Molecular Orbital No. 1:
--------------------------
Occupation: 2.000 Energy: -20.55028 a.u.
( 1 O 1s : 1.00)
Molecular Orbital No. 2:
--------------------------
Occupation: 2.000 Energy: -1.33471 a.u.
( 1 O 2s : 0.44) ( 1 O 3s : 0.38) ( 2 H 1s : 0.19)
( 3 H 1s : 0.19)
Molecular Orbital No. 3:
--------------------------
Occupation: 2.000 Energy: -0.69724 a.u.
( 1 O 1p+1: 0.49) ( 1 O 2p+1: 0.22) ( 2 H 1s : -0.33)
( 3 H 1s : 0.33)
Molecular Orbital No. 4:
--------------------------
Occupation: 2.000 Energy: -0.56644 a.u.
( 1 O 2s : -0.15) ( 1 O 3s : -0.35) ( 1 O 1p0 : -0.54)
( 1 O 2p0 : -0.37) ( 2 H 1s : 0.21) ( 3 H 1s : 0.21)
Molecular Orbital No. 5:
--------------------------
Occupation: 2.000 Energy: -0.49324 a.u.
( 1 O 1p-1: -0.63) ( 1 O 2p-1: -0.50)
Molecular Orbital No. 6:
--------------------------
Occupation: 0.000 Energy: 0.18437 a.u.
( 1 O 3s : 1.01) ( 1 O 1p0 : -0.19) ( 1 O 2p0 : -0.34)
( 2 H 2s : -0.83) ( 3 H 2s : -0.83)
Molecular Orbital No. 7:
--------------------------
Occupation: 0.000 Energy: 0.25556 a.u.
( 1 O 1p+1: -0.28) ( 1 O 2p+1: -0.67) ( 2 H 2s : -1.44)
( 3 H 2s : 1.44)
Molecular Orbital No. 8:
--------------------------
Occupation: 0.000 Energy: 0.78577 a.u.
( 1 O 1p+1: -0.27) ( 1 O 2p+1: -0.46) ( 2 H 1s : -0.94)
( 2 H 2s : 0.69) ( 2 H 1p0 : 0.15) ( 3 H 1s : 0.94)
( 3 H 2s : -0.69) ( 3 H 1p0 : -0.15)
Molecular Orbital No. 9:
--------------------------
Occupation: 0.000 Energy: 0.84995 a.u.
( 1 O 2s : 0.27) ( 1 O 3s : -0.35) ( 1 O 1p0 : -0.33)
( 2 H 1s : -0.78) ( 2 H 2s : 0.55) ( 2 H 1p+1: 0.29)
( 3 H 1s : -0.78) ( 3 H 2s : 0.55) ( 3 H 1p+1: -0.29)
Molecular Orbital No. 10:
--------------------------
Occupation: 0.000 Energy: 1.16230 a.u.
( 1 O 3s : 0.74) ( 1 O 1p0 : 0.76) ( 1 O 2p0 : -1.28)
( 2 H 1s : -0.54) ( 2 H 1p0 : -0.25) ( 3 H 1s : -0.54)
( 3 H 1p0 : -0.25)
Ground State Dipole Moment
----------------------------
X : 0.000000 a.u. 0.000000 Debye
Y : 0.000000 a.u. 0.000000 Debye
Z : -0.812127 a.u. -2.064221 Debye
Total : 0.812127 a.u. 2.064221 Debye
* Info * Checkpoint written to file: vlx_20240912_a9a42217.scf.h5
Self Consistent Field Driver Setup
====================================
Wave Function Model : Spin-Unrestricted Hartree-Fock
Initial Guess Model : Restart from Checkpoint
Convergence Accelerator : Direct Inversion of Iterative Subspace
Max. Number of Iterations : 50
Max. Number of Error Vectors : 10
Convergence Threshold : 1.0e-06
ERI Screening Scheme : Cauchy Schwarz + Density
ERI Screening Mode : Dynamic
ERI Screening Threshold : 1.0e-12
Linear Dependence Threshold : 1.0e-06
* Info * Nuclear repulsion energy: 9.1561447194 a.u.
* Info * Overlap matrix computed in 0.00 sec.
* Info * Kinetic energy matrix computed in 0.00 sec.
* Info * Nuclear potential matrix computed in 0.00 sec.
* Info * Orthogonalization matrix computed in 0.00 sec.
* Info * Restarting from checkpoint file: vlx_20240912_a9a42217.scf.h5
Iter. | Hartree-Fock Energy | Energy Change | Gradient Norm | Max. Gradient | Density Change
--------------------------------------------------------------------------------------------
1 -55.476698768014 0.0000000000 4.00725477 1.00603661 0.00000000
2 -56.031465126004 -0.5547663580 1.49516221 0.19142953 0.85523582
3 -56.177378495754 -0.1459133698 0.20617595 0.03128268 0.33481131
4 -56.180651358574 -0.0032728628 0.03175806 0.00523624 0.05436888
5 -56.180957941862 -0.0003065833 0.01110568 0.00195632 0.01691272
6 -56.181002534103 -0.0000445922 0.00267353 0.00047453 0.00810046
7 -56.181004700115 -0.0000021660 0.00061110 0.00007448 0.00172878
8 -56.181004792916 -0.0000000928 0.00009944 0.00001508 0.00036532
9 -56.181004794731 -0.0000000018 0.00001782 0.00000370 0.00005401
10 -56.181004794796 -0.0000000001 0.00000300 0.00000068 0.00000901
11 -56.181004794798 -0.0000000000 0.00000076 0.00000011 0.00000154
* Info * Checkpoint written to file: vlx_20240912_a9a42217.scf.h5
* Info * SCF results written to file: vlx_20240912_a9a42217.scf.results.h5
*** SCF converged in 11 iterations. Time: 0.61 sec.
Spin-Unrestricted Hartree-Fock:
-------------------------------
Total Energy : -56.1810047948 a.u.
Electronic Energy : -65.3371495142 a.u.
Nuclear Repulsion Energy : 9.1561447194 a.u.
------------------------------------
Gradient Norm : 0.0000007610 a.u.
Ground State Information
------------------------
Charge of Molecule : 1.0
Magnetic Quantum Number (M_S) : 0.5
Expectation value of S**2 : 0.7648
Spin Unrestricted Alpha Orbitals
--------------------------------
Molecular Orbital No. 1:
--------------------------
Occupation: 1.000 Energy: -24.02738 a.u.
( 1 O 1s : 1.06)
Molecular Orbital No. 2:
--------------------------
Occupation: 1.000 Energy: -2.02457 a.u.
( 1 O 2s : 0.63) ( 1 O 3s : 0.27) ( 2 H 1s : 0.15)
( 3 H 1s : 0.15)
Molecular Orbital No. 3:
--------------------------
Occupation: 1.000 Energy: -1.32957 a.u.
( 1 O 1p+1: 0.70) ( 1 O 2p+1: 0.17) ( 2 H 1s : -0.24)
( 3 H 1s : 0.24)
Molecular Orbital No. 4:
--------------------------
Occupation: 1.000 Energy: -1.23386 a.u.
( 1 O 2s : -0.18) ( 1 O 3s : -0.18) ( 1 O 1p0 : -0.74)
( 1 O 2p0 : -0.22) ( 2 H 1s : 0.15) ( 3 H 1s : 0.15)
Molecular Orbital No. 5:
--------------------------
Occupation: 1.000 Energy: -1.18294 a.u.
( 1 O 1p-1: -0.81) ( 1 O 2p-1: -0.28)
Molecular Orbital No. 6:
--------------------------
Occupation: 0.000 Energy: -0.17239 a.u.
( 1 O 2s : 0.18) ( 1 O 3s : 0.77) ( 1 O 1p0 : -0.23)
( 1 O 2p0 : -0.19) ( 2 H 1s : -0.18) ( 2 H 2s : -0.70)
( 3 H 1s : -0.18) ( 3 H 2s : -0.70)
Molecular Orbital No. 7:
--------------------------
Occupation: 0.000 Energy: -0.10078 a.u.
( 1 O 1p+1: -0.35) ( 1 O 2p+1: -0.45) ( 2 H 1s : -0.23)
( 2 H 2s : -1.17) ( 3 H 1s : 0.23) ( 3 H 2s : 1.17)
Molecular Orbital No. 8:
--------------------------
Occupation: 0.000 Energy: 0.37249 a.u.
( 1 O 1p+1: -0.32) ( 2 H 1s : -0.90) ( 2 H 2s : 1.06)
( 3 H 1s : 0.90) ( 3 H 2s : -1.06)
Molecular Orbital No. 9:
--------------------------
Occupation: 0.000 Energy: 0.39727 a.u.
( 1 O 2s : 0.28) ( 1 O 3s : -0.59) ( 1 O 1p0 : -0.43)
( 1 O 2p0 : 0.38) ( 2 H 1s : -0.69) ( 2 H 2s : 0.69)
( 2 H 1p+1: 0.23) ( 3 H 1s : -0.69) ( 3 H 2s : 0.69)
( 3 H 1p+1: -0.23)
Molecular Orbital No. 10:
--------------------------
Occupation: 0.000 Energy: 0.59798 a.u.
( 1 O 1p-1: -0.82) ( 1 O 2p-1: 1.08)
Spin Unrestricted Beta Orbitals
-------------------------------
Molecular Orbital No. 1:
--------------------------
Occupation: 1.000 Energy: -1.90790 a.u.
( 1 O 2s : 0.55) ( 1 O 3s : 0.31) ( 2 H 1s : 0.18)
( 3 H 1s : 0.18)
Molecular Orbital No. 2:
--------------------------
Occupation: 1.000 Energy: -1.26787 a.u.
( 1 O 1p+1: 0.64) ( 1 O 2p+1: 0.18) ( 2 H 1s : -0.28)
( 3 H 1s : 0.28)
Molecular Orbital No. 3:
--------------------------
Occupation: 1.000 Energy: -1.15789 a.u.
( 1 O 2s : -0.18) ( 1 O 3s : -0.24) ( 1 O 1p0 : -0.69)
( 1 O 2p0 : -0.26) ( 2 H 1s : 0.17) ( 3 H 1s : 0.17)
Molecular Orbital No. 4:
--------------------------
Occupation: 1.000 Energy: -1.10427 a.u.
( 1 O 1p-1: -0.77) ( 1 O 2p-1: -0.33)
Molecular Orbital No. 5:
--------------------------
Occupation: 0.000 Energy: -19.14601 a.u.
( 1 O 1s : 1.00)
Molecular Orbital No. 6:
--------------------------
Occupation: 0.000 Energy: -0.15857 a.u.
( 1 O 2s : 0.16) ( 1 O 3s : 0.83) ( 1 O 1p0 : -0.23)
( 1 O 2p0 : -0.22) ( 2 H 1s : -0.17) ( 2 H 2s : -0.73)
( 3 H 1s : -0.17) ( 3 H 2s : -0.73)
Molecular Orbital No. 7:
--------------------------
Occupation: 0.000 Energy: -0.08775 a.u.
( 1 O 1p+1: -0.36) ( 1 O 2p+1: -0.51) ( 2 H 1s : -0.20)
( 2 H 2s : -1.20) ( 3 H 1s : 0.20) ( 3 H 2s : 1.20)
Molecular Orbital No. 8:
--------------------------
Occupation: 0.000 Energy: 0.36931 a.u.
( 1 O 1p+1: -0.30) ( 1 O 2p+1: -0.16) ( 2 H 1s : -0.92)
( 2 H 2s : 1.00) ( 3 H 1s : 0.92) ( 3 H 2s : -1.00)
Molecular Orbital No. 9:
--------------------------
Occupation: 0.000 Energy: 0.40896 a.u.
( 1 O 2s : 0.26) ( 1 O 3s : -0.49) ( 1 O 1p0 : -0.41)
( 1 O 2p0 : 0.25) ( 2 H 1s : -0.74) ( 2 H 2s : 0.67)
( 2 H 1p+1: 0.24) ( 3 H 1s : -0.74) ( 3 H 2s : 0.67)
( 3 H 1p+1: -0.24)
Ground State Dipole Moment
----------------------------
*** Warning: Molecule has non-zero charge. Dipole
moment will be dependent on the choice of origin.
Center of nuclear charge is chosen as the origin.
X : -0.000000 a.u. -0.000000 Debye
Y : 0.000000 a.u. 0.000000 Debye
Z : -1.063185 a.u. -2.702348 Debye
Total : 1.063185 a.u. 2.702348 Debye
* Info * Reading basis set from file: /home/emi/miniconda3/envs/echem/lib/python3.11/site-packages/veloxchem/basis/CC-PCVDZ
Molecular Basis (Atomic Basis)
================================
Basis: CC-PCVDZ
Atom Contracted GTOs Primitive GTOs
H (2S,1P) (4S,1P)
F (4S,3P,1D) (18S,5P,1D)
Contracted Basis Functions : 23
Primitive Basis Functions : 45
Self Consistent Field Driver Setup
====================================
Wave Function Model : Spin-Restricted Hartree-Fock
Initial Guess Model : Superposition of Atomic Densities
Convergence Accelerator : Two Level Direct Inversion of Iterative Subspace
Max. Number of Iterations : 50
Max. Number of Error Vectors : 10
Convergence Threshold : 1.0e-06
ERI Screening Scheme : Cauchy Schwarz + Density
ERI Screening Mode : Dynamic
ERI Screening Threshold : 1.0e-12
Linear Dependence Threshold : 1.0e-06
* Info * Nuclear repulsion energy: 5.1881022960 a.u.
* Info * Overlap matrix computed in 0.00 sec.
* Info * Kinetic energy matrix computed in 0.00 sec.
* Info * Nuclear potential matrix computed in 0.00 sec.
* Info * Orthogonalization matrix computed in 0.00 sec.
* Info * SAD initial guess computed in 0.00 sec.
* Info * Starting Reduced Basis SCF calculation...
* Info * ...done. SCF energy in reduced basis set: -99.988874777753 a.u. Time: 0.03 sec.
* Info * Overlap matrix computed in 0.00 sec.
* Info * Kinetic energy matrix computed in 0.00 sec.
* Info * Nuclear potential matrix computed in 0.00 sec.
* Info * Orthogonalization matrix computed in 0.00 sec.
Iter. | Hartree-Fock Energy | Energy Change | Gradient Norm | Max. Gradient | Density Change
--------------------------------------------------------------------------------------------
1 -100.018768000114 0.0000000000 0.09773637 0.01303368 0.00000000
2 -100.019585862254 -0.0008178621 0.02190606 0.00305029 0.02171836
3 -100.019640824607 -0.0000549624 0.00566262 0.00116714 0.00487750
4 -100.019645492095 -0.0000046675 0.00331753 0.00040072 0.00201343
5 -100.019646381262 -0.0000008892 0.00037277 0.00005411 0.00064692
6 -100.019646410026 -0.0000000288 0.00003872 0.00000711 0.00017580
7 -100.019646410326 -0.0000000003 0.00000210 0.00000036 0.00001858
8 -100.019646410327 -0.0000000000 0.00000019 0.00000003 0.00000071
*** SCF converged in 8 iterations. Time: 0.50 sec.
Spin-Restricted Hartree-Fock:
-----------------------------
Total Energy : -100.0196464103 a.u.
Electronic Energy : -105.2077487064 a.u.
Nuclear Repulsion Energy : 5.1881022960 a.u.
------------------------------------
Gradient Norm : 0.0000001942 a.u.
Ground State Information
------------------------
Charge of Molecule : 0.0
Multiplicity (2S+1) : 1.0
Magnetic Quantum Number (M_S) : 0.0
Spin Restricted Orbitals
------------------------
Molecular Orbital No. 1:
--------------------------
Occupation: 2.000 Energy: -26.27716 a.u.
( 2 F 1s : 1.00)
Molecular Orbital No. 2:
--------------------------
Occupation: 2.000 Energy: -1.58313 a.u.
( 1 H 1s : 0.17) ( 2 F 2s : 0.48) ( 2 F 3s : 0.48)
Molecular Orbital No. 3:
--------------------------
Occupation: 2.000 Energy: -0.74719 a.u.
( 1 H 1s : 0.39) ( 2 F 3s : -0.29) ( 2 F 1p0 : -0.56)
( 2 F 2p0 : -0.30)
Molecular Orbital No. 4:
--------------------------
Occupation: 2.000 Energy: -0.62915 a.u.
( 2 F 1p-1: 0.66) ( 2 F 2p-1: 0.47)
Molecular Orbital No. 5:
--------------------------
Occupation: 2.000 Energy: -0.62915 a.u.
( 2 F 1p+1: 0.66) ( 2 F 2p+1: 0.47)
Molecular Orbital No. 6:
--------------------------
Occupation: 0.000 Energy: 0.18337 a.u.
( 1 H 2s : -1.27) ( 2 F 3s : 0.67) ( 2 F 1p0 : -0.22)
( 2 F 2p0 : -0.34)
Molecular Orbital No. 7:
--------------------------
Occupation: 0.000 Energy: 0.80873 a.u.
( 1 H 1s : -1.27) ( 1 H 2s : 0.91) ( 1 H 1p0 : 0.33)
( 2 F 1p0 : -0.37) ( 2 F 2p0 : -0.19)
Molecular Orbital No. 8:
--------------------------
Occupation: 0.000 Energy: 1.40908 a.u.
( 1 H 1p-1: 0.43) ( 2 F 1p-1: -0.85) ( 2 F 2p-1: 0.75)
Molecular Orbital No. 9:
--------------------------
Occupation: 0.000 Energy: 1.40908 a.u.
( 1 H 1p+1: 0.43) ( 2 F 1p+1: -0.85) ( 2 F 2p+1: 0.75)
Molecular Orbital No. 10:
--------------------------
Occupation: 0.000 Energy: 1.41388 a.u.
( 1 H 1s : -1.07) ( 1 H 1p0 : -0.51) ( 2 F 2s : 0.24)
( 2 F 3s : 0.57) ( 2 F 1p0 : 0.65) ( 2 F 2p0 : -1.61)
Ground State Dipole Moment
----------------------------
X : -0.000000 a.u. -0.000000 Debye
Y : -0.000000 a.u. -0.000000 Debye
Z : -0.768372 a.u. -1.953007 Debye
Total : 0.768372 a.u. 1.953007 Debye
* Info * Checkpoint written to file: vlx_20240912_0a787337.scf.h5
Self Consistent Field Driver Setup
====================================
Wave Function Model : Spin-Unrestricted Hartree-Fock
Initial Guess Model : Restart from Checkpoint
Convergence Accelerator : Direct Inversion of Iterative Subspace
Max. Number of Iterations : 50
Max. Number of Error Vectors : 10
Convergence Threshold : 1.0e-06
ERI Screening Scheme : Cauchy Schwarz + Density
ERI Screening Mode : Dynamic
ERI Screening Threshold : 1.0e-12
Linear Dependence Threshold : 1.0e-06
* Info * Nuclear repulsion energy: 5.1881022960 a.u.
* Info * Overlap matrix computed in 0.00 sec.
* Info * Kinetic energy matrix computed in 0.00 sec.
* Info * Nuclear potential matrix computed in 0.00 sec.
* Info * Orthogonalization matrix computed in 0.00 sec.
* Info * Restarting from checkpoint file: vlx_20240912_0a787337.scf.h5
Iter. | Hartree-Fock Energy | Energy Change | Gradient Norm | Max. Gradient | Density Change
--------------------------------------------------------------------------------------------
1 -73.742490771103 0.0000000000 4.65394692 1.19371628 0.00000000
2 -74.398937627258 -0.6564468562 1.45174136 0.15266049 0.80606973
3 -74.507809858140 -0.1088722309 0.15003366 0.02152883 0.27290087
4 -74.509195127826 -0.0013852697 0.02481321 0.00345443 0.03446813
5 -74.509328657671 -0.0001335298 0.00650857 0.00110570 0.01088816
6 -74.509339136024 -0.0000104784 0.00159980 0.00028573 0.00336728
7 -74.509339787444 -0.0000006514 0.00032453 0.00004058 0.00089691
8 -74.509339810128 -0.0000000227 0.00004148 0.00000612 0.00018196
9 -74.509339810308 -0.0000000002 0.00000481 0.00000071 0.00001225
10 -74.509339810311 -0.0000000000 0.00000052 0.00000010 0.00000206
* Info * Checkpoint written to file: vlx_20240912_0a787337.scf.h5
* Info * SCF results written to file: vlx_20240912_0a787337.scf.results.h5
*** SCF converged in 10 iterations. Time: 0.62 sec.
Spin-Unrestricted Hartree-Fock:
-------------------------------
Total Energy : -74.5093398103 a.u.
Electronic Energy : -79.6974421063 a.u.
Nuclear Repulsion Energy : 5.1881022960 a.u.
------------------------------------
Gradient Norm : 0.0000005166 a.u.
Ground State Information
------------------------
Charge of Molecule : 1.0
Magnetic Quantum Number (M_S) : 0.5
Expectation value of S**2 : 0.7589
Spin Unrestricted Alpha Orbitals
--------------------------------
Molecular Orbital No. 1:
--------------------------
Occupation: 1.000 Energy: -30.25722 a.u.
( 2 F 1s : 1.05)
Molecular Orbital No. 2:
--------------------------
Occupation: 1.000 Energy: -2.41524 a.u.
( 2 F 2s : 0.65) ( 2 F 3s : 0.34)
Molecular Orbital No. 3:
--------------------------
Occupation: 1.000 Energy: -1.54540 a.u.
( 1 H 1s : 0.27) ( 2 F 3s : -0.16) ( 2 F 1p0 : -0.75)
( 2 F 2p0 : -0.19)
Molecular Orbital No. 4:
--------------------------
Occupation: 1.000 Energy: -1.46185 a.u.
( 2 F 1p-1: 0.82) ( 2 F 2p-1: 0.27)
Molecular Orbital No. 5:
--------------------------
Occupation: 1.000 Energy: -1.46185 a.u.
( 2 F 1p+1: 0.82) ( 2 F 2p+1: 0.27)
Molecular Orbital No. 6:
--------------------------
Occupation: 0.000 Energy: -0.21792 a.u.
( 1 H 1s : -0.36) ( 1 H 2s : -1.01) ( 2 F 3s : 0.50)
( 2 F 1p0 : -0.26) ( 2 F 2p0 : -0.21)
Molecular Orbital No. 7:
--------------------------
Occupation: 0.000 Energy: 0.30737 a.u.
( 1 H 1s : -1.18) ( 1 H 2s : 1.15) ( 1 H 1p0 : 0.25)
( 2 F 3s : -0.26) ( 2 F 1p0 : -0.38)
Molecular Orbital No. 8:
--------------------------
Occupation: 0.000 Energy: 0.73464 a.u.
( 1 H 1p-1: 0.25) ( 2 F 1p-1: -0.77) ( 2 F 2p-1: 0.97)
Molecular Orbital No. 9:
--------------------------
Occupation: 0.000 Energy: 0.73464 a.u.
( 1 H 1p+1: 0.25) ( 2 F 1p+1: -0.77) ( 2 F 2p+1: 0.97)
Molecular Orbital No. 10:
--------------------------
Occupation: 0.000 Energy: 0.84884 a.u.
( 1 H 1s : -1.05) ( 1 H 1p0 : -0.29) ( 2 F 2s : 0.37)
( 2 F 3s : 0.18) ( 2 F 1p0 : 0.56) ( 2 F 2p0 : -1.54)
Spin Unrestricted Beta Orbitals
-------------------------------
Molecular Orbital No. 1:
--------------------------
Occupation: 1.000 Energy: -2.28147 a.u.
( 1 H 1s : 0.15) ( 2 F 2s : 0.59) ( 2 F 3s : 0.40)
Molecular Orbital No. 2:
--------------------------
Occupation: 1.000 Energy: -1.46527 a.u.
( 1 H 1s : 0.31) ( 2 F 3s : -0.20) ( 2 F 1p0 : -0.71)
( 2 F 2p0 : -0.21)
Molecular Orbital No. 3:
--------------------------
Occupation: 1.000 Energy: -1.37679 a.u.
( 2 F 1p+1: -0.60) ( 2 F 1p-1: 0.52) ( 2 F 2p+1: -0.24)
( 2 F 2p-1: 0.21)
Molecular Orbital No. 4:
--------------------------
Occupation: 1.000 Energy: -1.37679 a.u.
( 2 F 1p+1: 0.52) ( 2 F 1p-1: 0.60) ( 2 F 2p+1: 0.21)
( 2 F 2p-1: 0.24)
Molecular Orbital No. 5:
--------------------------
Occupation: 0.000 Energy: -24.76185 a.u.
( 2 F 1s : 1.00)
Molecular Orbital No. 6:
--------------------------
Occupation: 0.000 Energy: -0.20513 a.u.
( 1 H 1s : -0.34) ( 1 H 2s : -1.04) ( 2 F 3s : 0.54)
( 2 F 1p0 : -0.27) ( 2 F 2p0 : -0.23)
Molecular Orbital No. 7:
--------------------------
Occupation: 0.000 Energy: 0.31497 a.u.
( 1 H 1s : -1.22) ( 1 H 2s : 1.13) ( 1 H 1p0 : 0.26)
( 2 F 3s : -0.22) ( 2 F 1p0 : -0.38)
Molecular Orbital No. 8:
--------------------------
Occupation: 0.000 Energy: 0.77758 a.u.
( 1 H 1p-1: 0.25) ( 2 F 1p+1: -0.39) ( 2 F 1p-1: -0.69)
( 2 F 2p+1: 0.46) ( 2 F 2p-1: 0.81)
Molecular Orbital No. 9:
--------------------------
Occupation: 0.000 Energy: 0.77758 a.u.
( 1 H 1p+1: 0.25) ( 2 F 1p+1: -0.69) ( 2 F 1p-1: 0.39)
( 2 F 2p+1: 0.81) ( 2 F 2p-1: -0.46)
Ground State Dipole Moment
----------------------------
*** Warning: Molecule has non-zero charge. Dipole
moment will be dependent on the choice of origin.
Center of nuclear charge is chosen as the origin.
X : -0.000000 a.u. -0.000000 Debye
Y : 0.000000 a.u. 0.000000 Debye
Z : -0.993424 a.u. -2.525032 Debye
Total : 0.993424 a.u. 2.525032 Debye
* Info * Reading basis set from file: /home/emi/miniconda3/envs/echem/lib/python3.11/site-packages/veloxchem/basis/CC-PCVDZ
Molecular Basis (Atomic Basis)
================================
Basis: CC-PCVDZ
Atom Contracted GTOs Primitive GTOs
Ne (4S,3P,1D) (18S,5P,1D)
Contracted Basis Functions : 18
Primitive Basis Functions : 38
Self Consistent Field Driver Setup
====================================
Wave Function Model : Spin-Restricted Hartree-Fock
Initial Guess Model : Superposition of Atomic Densities
Convergence Accelerator : Two Level Direct Inversion of Iterative Subspace
Max. Number of Iterations : 50
Max. Number of Error Vectors : 10
Convergence Threshold : 1.0e-06
ERI Screening Scheme : Cauchy Schwarz + Density
ERI Screening Mode : Dynamic
ERI Screening Threshold : 1.0e-12
Linear Dependence Threshold : 1.0e-06
* Info * Nuclear repulsion energy: 0.0000000000 a.u.
* Info * Overlap matrix computed in 0.00 sec.
* Info * Kinetic energy matrix computed in 0.00 sec.
* Info * Nuclear potential matrix computed in 0.00 sec.
* Info * Orthogonalization matrix computed in 0.00 sec.
* Info * SAD initial guess computed in 0.00 sec.
* Info * Starting Reduced Basis SCF calculation...
* Info * ...done. SCF energy in reduced basis set: -128.488925926667 a.u. Time: 0.02 sec.
* Info * Overlap matrix computed in 0.00 sec.
* Info * Kinetic energy matrix computed in 0.00 sec.
* Info * Nuclear potential matrix computed in 0.00 sec.
* Info * Orthogonalization matrix computed in 0.00 sec.
Iter. | Hartree-Fock Energy | Energy Change | Gradient Norm | Max. Gradient | Density Change
--------------------------------------------------------------------------------------------
1 -128.488925929027 0.0000000000 0.00008363 0.00002132 0.00000000
2 -128.488925929352 -0.0000000003 0.00001743 0.00000273 0.00001389
3 -128.488925929372 -0.0000000000 0.00000043 0.00000014 0.00000294
*** SCF converged in 3 iterations. Time: 0.28 sec.
Spin-Restricted Hartree-Fock:
-----------------------------
Total Energy : -128.4889259294 a.u.
Electronic Energy : -128.4889259294 a.u.
Nuclear Repulsion Energy : 0.0000000000 a.u.
------------------------------------
Gradient Norm : 0.0000004282 a.u.
Ground State Information
------------------------
Charge of Molecule : 0.0
Multiplicity (2S+1) : 1.0
Magnetic Quantum Number (M_S) : 0.0
Spin Restricted Orbitals
------------------------
Molecular Orbital No. 1:
--------------------------
Occupation: 2.000 Energy: -32.76419 a.u.
( 1 Ne 1s : -1.00)
Molecular Orbital No. 2:
--------------------------
Occupation: 2.000 Energy: -1.91886 a.u.
( 1 Ne 2s : -0.52) ( 1 Ne 3s : -0.57)
Molecular Orbital No. 3:
--------------------------
Occupation: 2.000 Energy: -0.83240 a.u.
( 1 Ne 1p+1: -0.64) ( 1 Ne 1p0 : 0.24) ( 1 Ne 2p+1: -0.42)
( 1 Ne 2p0 : 0.16)
Molecular Orbital No. 4:
--------------------------
Occupation: 2.000 Energy: -0.83240 a.u.
( 1 Ne 1p+1: -0.24) ( 1 Ne 1p-1: -0.55) ( 1 Ne 1p0 : -0.35)
( 1 Ne 2p+1: -0.16) ( 1 Ne 2p-1: -0.36) ( 1 Ne 2p0 : -0.23)
Molecular Orbital No. 5:
--------------------------
Occupation: 2.000 Energy: -0.83240 a.u.
( 1 Ne 1p-1: 0.41) ( 1 Ne 1p0 : -0.55) ( 1 Ne 2p-1: 0.27)
( 1 Ne 2p0 : -0.36)
Molecular Orbital No. 6:
--------------------------
Occupation: 0.000 Energy: 1.69054 a.u.
( 1 Ne 1p+1: 0.18) ( 1 Ne 1p0 : 0.88) ( 1 Ne 2p+1: -0.20)
( 1 Ne 2p-1: 0.15) ( 1 Ne 2p0 : -1.02)
Molecular Orbital No. 7:
--------------------------
Occupation: 0.000 Energy: 1.69054 a.u.
( 1 Ne 1p+1: -0.82) ( 1 Ne 1p-1: 0.32) ( 1 Ne 1p0 : 0.21)
( 1 Ne 2p+1: 0.95) ( 1 Ne 2p-1: -0.37) ( 1 Ne 2p0 : -0.25)
Molecular Orbital No. 8:
--------------------------
Occupation: 0.000 Energy: 1.69054 a.u.
( 1 Ne 1p+1: -0.35) ( 1 Ne 1p-1: -0.84) ( 1 Ne 2p+1: 0.40)
( 1 Ne 2p-1: 0.97)
Molecular Orbital No. 9:
--------------------------
Occupation: 0.000 Energy: 2.09313 a.u.
( 1 Ne 1s : -0.52) ( 1 Ne 2s : -1.52) ( 1 Ne 3s : 1.51)
Molecular Orbital No. 10:
--------------------------
Occupation: 0.000 Energy: 5.19630 a.u.
( 1 Ne 1d+1: -0.83) ( 1 Ne 1d+2: 0.23) ( 1 Ne 1d0 : 0.48)
Ground State Dipole Moment
----------------------------
X : 0.000000 a.u. 0.000000 Debye
Y : 0.000000 a.u. 0.000000 Debye
Z : -0.000000 a.u. -0.000000 Debye
Total : 0.000000 a.u. 0.000000 Debye
* Info * Checkpoint written to file: vlx_20240912_5cb12842.scf.h5
Self Consistent Field Driver Setup
====================================
Wave Function Model : Spin-Unrestricted Hartree-Fock
Initial Guess Model : Restart from Checkpoint
Convergence Accelerator : Direct Inversion of Iterative Subspace
Max. Number of Iterations : 50
Max. Number of Error Vectors : 10
Convergence Threshold : 1.0e-06
ERI Screening Scheme : Cauchy Schwarz + Density
ERI Screening Mode : Dynamic
ERI Screening Threshold : 1.0e-12
Linear Dependence Threshold : 1.0e-06
* Info * Nuclear repulsion energy: 0.0000000000 a.u.
* Info * Overlap matrix computed in 0.00 sec.
* Info * Kinetic energy matrix computed in 0.00 sec.
* Info * Nuclear potential matrix computed in 0.00 sec.
* Info * Orthogonalization matrix computed in 0.00 sec.
* Info * Restarting from checkpoint file: vlx_20240912_5cb12842.scf.h5
Iter. | Hartree-Fock Energy | Energy Change | Gradient Norm | Max. Gradient | Density Change
--------------------------------------------------------------------------------------------
1 -95.724739415048 0.0000000000 5.28148132 1.26602289 0.00000000
2 -96.447251770784 -0.7225123557 1.28775994 0.20942739 0.73277939
3 -96.508840201458 -0.0615884307 0.08798008 0.01988639 0.19104619
4 -96.509196421834 -0.0003562204 0.01626179 0.00327620 0.01701992
5 -96.509231483788 -0.0000350620 0.00285999 0.00052555 0.00566536
6 -96.509232485076 -0.0000010013 0.00010250 0.00003847 0.00110714
7 -96.509232486360 -0.0000000013 0.00001338 0.00000395 0.00004150
8 -96.509232486370 -0.0000000000 0.00000063 0.00000011 0.00000278
* Info * Checkpoint written to file: vlx_20240912_5cb12842.scf.h5
* Info * SCF results written to file: vlx_20240912_5cb12842.scf.results.h5
*** SCF converged in 8 iterations. Time: 0.51 sec.
Spin-Unrestricted Hartree-Fock:
-------------------------------
Total Energy : -96.5092324864 a.u.
Electronic Energy : -96.5092324864 a.u.
Nuclear Repulsion Energy : 0.0000000000 a.u.
------------------------------------
Gradient Norm : 0.0000006335 a.u.
Ground State Information
------------------------
Charge of Molecule : 1.0
Magnetic Quantum Number (M_S) : 0.5
Expectation value of S**2 : 0.7549
Spin Unrestricted Alpha Orbitals
--------------------------------
Molecular Orbital No. 1:
--------------------------
Occupation: 1.000 Energy: -37.33903 a.u.
( 1 Ne 1s : -1.04)
Molecular Orbital No. 2:
--------------------------
Occupation: 1.000 Energy: -2.94250 a.u.
( 1 Ne 2s : -0.68) ( 1 Ne 3s : -0.39)
Molecular Orbital No. 3:
--------------------------
Occupation: 1.000 Energy: -1.86722 a.u.
( 1 Ne 1p-1: 0.84) ( 1 Ne 2p-1: 0.26)
Molecular Orbital No. 4:
--------------------------
Occupation: 1.000 Energy: -1.86722 a.u.
( 1 Ne 1p+1: -0.28) ( 1 Ne 1p0 : -0.79) ( 1 Ne 2p0 : -0.24)
Molecular Orbital No. 5:
--------------------------
Occupation: 1.000 Energy: -1.86722 a.u.
( 1 Ne 1p+1: 0.80) ( 1 Ne 1p0 : -0.28) ( 1 Ne 2p+1: 0.24)
Molecular Orbital No. 6:
--------------------------
Occupation: 0.000 Energy: 0.89666 a.u.
( 1 Ne 1p+1: 0.73) ( 1 Ne 1p-1: 0.20) ( 1 Ne 2p+1: -1.07)
( 1 Ne 2p-1: -0.29)
Molecular Orbital No. 7:
--------------------------
Occupation: 0.000 Energy: 0.89666 a.u.
( 1 Ne 1p-1: 0.60) ( 1 Ne 1p0 : -0.46) ( 1 Ne 2p+1: 0.16)
( 1 Ne 2p-1: -0.88) ( 1 Ne 2p0 : 0.66)
Molecular Orbital No. 8:
--------------------------
Occupation: 0.000 Energy: 0.89666 a.u.
( 1 Ne 1p+1: 0.19) ( 1 Ne 1p-1: -0.43) ( 1 Ne 1p0 : -0.61)
( 1 Ne 2p+1: -0.27) ( 1 Ne 2p-1: 0.62) ( 1 Ne 2p0 : 0.88)
Molecular Orbital No. 9:
--------------------------
Occupation: 0.000 Energy: 1.25223 a.u.
( 1 Ne 1s : -0.50) ( 1 Ne 2s : -1.45) ( 1 Ne 3s : 1.56)
Molecular Orbital No. 10:
--------------------------
Occupation: 0.000 Energy: 4.43099 a.u.
( 1 Ne 1d+1: -0.37) ( 1 Ne 1d+2: -0.74) ( 1 Ne 1d-1: -0.32)
( 1 Ne 1d-2: 0.42) ( 1 Ne 1d0 : 0.21)
Spin Unrestricted Beta Orbitals
-------------------------------
Molecular Orbital No. 1:
--------------------------
Occupation: 1.000 Energy: -2.79165 a.u.
( 1 Ne 2s : -0.63) ( 1 Ne 3s : -0.45)
Molecular Orbital No. 2:
--------------------------
Occupation: 1.000 Energy: -1.77472 a.u.
( 1 Ne 1p+1: -0.80) ( 1 Ne 1p-1: 0.17) ( 1 Ne 2p+1: -0.29)
Molecular Orbital No. 3:
--------------------------
Occupation: 1.000 Energy: -1.77472 a.u.
( 1 Ne 1p+1: -0.17) ( 1 Ne 1p-1: -0.78) ( 1 Ne 1p0 : -0.19)
( 1 Ne 2p-1: -0.28)
Molecular Orbital No. 4:
--------------------------
Occupation: 1.000 Energy: -1.77472 a.u.
( 1 Ne 1p-1: 0.19) ( 1 Ne 1p0 : -0.80) ( 1 Ne 2p0 : -0.29)
Molecular Orbital No. 5:
--------------------------
Occupation: 0.000 Energy: -31.22975 a.u.
( 1 Ne 1s : -1.00)
Molecular Orbital No. 6:
--------------------------
Occupation: 0.000 Energy: 0.94282 a.u.
( 1 Ne 1p+1: 0.33) ( 1 Ne 1p-1: -0.36) ( 1 Ne 1p0 : 0.63)
( 1 Ne 2p+1: -0.46) ( 1 Ne 2p-1: 0.50) ( 1 Ne 2p0 : -0.87)
Molecular Orbital No. 7:
--------------------------
Occupation: 0.000 Energy: 0.94282 a.u.
( 1 Ne 1p+1: -0.70) ( 1 Ne 1p0 : 0.38) ( 1 Ne 2p+1: 0.97)
( 1 Ne 2p0 : -0.53)
Molecular Orbital No. 8:
--------------------------
Occupation: 0.000 Energy: 0.94282 a.u.
( 1 Ne 1p+1: -0.19) ( 1 Ne 1p-1: -0.71) ( 1 Ne 1p0 : -0.31)
( 1 Ne 2p+1: 0.26) ( 1 Ne 2p-1: 0.98) ( 1 Ne 2p0 : 0.43)
Molecular Orbital No. 9:
--------------------------
Occupation: 0.000 Energy: 1.35039 a.u.
( 1 Ne 1s : -0.50) ( 1 Ne 2s : -1.48) ( 1 Ne 3s : 1.55)
Ground State Dipole Moment
----------------------------
*** Warning: Molecule has non-zero charge. Dipole
moment will be dependent on the choice of origin.
Center of nuclear charge is chosen as the origin.
X : 0.000000 a.u. 0.000000 Debye
Y : 0.000000 a.u. 0.000000 Debye
Z : -0.000000 a.u. -0.000000 Debye
Total : 0.000000 a.u. 0.000000 Debye
plt.figure(figsize=(6, 4))
# Plot error from MO energies and delta-SCF
plt.plot([1, 2, 3, 4, 5], err_koopman, "bs")
plt.plot([1, 2, 3, 4, 5], err_delta, "ro")
plt.plot([0.5, 5.5], [0, 0], "k--", zorder=0)
plt.legend(("Koopmans' theorem", r"$\Delta$SCF"))
plt.ylabel("Error wrt experiment [eV]")
plt.xticks([1, 2, 3, 4, 5], (r"CH$_4$", r"NH$_3$", r"H$_2$O", "HF", "Ne"))
plt.xlim((0.5, 5.5))
plt.tight_layout()
plt.show()
We see that the error from orbital energies is large (14.4-22.3 eV) and clearly scales with atomic number, while the error of \(\Delta\)SCF remains small (absolute error of 0.15-0.38 eV).
Including relaxation with wave-function methods#
Considering the X-ray absorption and emission spectrum of water, the error of ADC(n) calculations with respect to experimental measurements can be considered:
Note
Currently using pyscf – this will be updated.
# Create pyscf mol object
mol = gto.Mole()
mol.atom = water_mol_str
mol.basis = "unc-6-31G"
mol.build()
# Perform restricted SCF calculation
scf_gs = scf.RHF(mol)
scf_gs.kernel()
# Perform CVS-ADC calculations
xas_adc1 = adcc.cvs_adc1(scf_gs, n_singlets=2, core_orbitals=1)
xas_adc2 = adcc.cvs_adc2(scf_gs, n_singlets=2, core_orbitals=1)
xas_adc2x = adcc.cvs_adc2x(scf_gs, n_singlets=2, core_orbitals=1)
xas_adc3 = adcc.cvs_adc3(scf_gs, n_singlets=2, core_orbitals=1)
# Perform unrestricted SCF calculation
scf_gs = scf.UHF(mol)
scf_gs.kernel()
# Copy molecular orbitals
mo0 = copy.deepcopy(scf_gs.mo_coeff)
occ0 = copy.deepcopy(scf_gs.mo_occ)
# Create 1s core-hole by setting alpha_0 population to zero
occ0[0][0] = 0.0
# Perform unrestricted SCF calculation with MOM constraint
scf_ion = scf.UHF(mol)
scf.addons.mom_occ(scf_ion, mo0, occ0)
scf_ion.kernel()
# Perform ADC calculations
xes_adc1 = adcc.adc1(scf_ion, n_states=2)
xes_adc2 = adcc.adc2(scf_ion, n_states=2)
xes_adc2x = adcc.adc2x(scf_ion, n_states=2)
xes_adc3 = adcc.adc3(scf_ion, n_states=2)
Plotting the errors compared to experiment (given as a dashed line), and the variations in oscillator strength:
plt.figure(figsize=(10, 6))
plt.subplot(221)
plt.title("XAS energy")
expt, rel = 534.00, 0.37
plt.plot(0, au2ev * xas_adc1.excitation_energy[0] + rel - expt, "bo")
plt.plot(1, au2ev * xas_adc2.excitation_energy[0] + rel - expt, "bo")
plt.plot(2, au2ev * xas_adc2x.excitation_energy[0] + rel - expt, "bo")
plt.plot(3, au2ev * xas_adc3.excitation_energy[0] + rel - expt, "bo")
plt.plot([-0.5, 3.5], [0, 0], "k--", zorder=0)
plt.xlim((-0.5, 3.5))
plt.ylabel("Error wrt experiment [eV]")
plt.xticks([0, 1, 2, 3], ("ADC(1)", "ADC(2)", "ADC(2)-x", "ADC(3/2)"))
plt.subplot(222)
plt.title("XAS oscillator strength")
plt.plot(0, xas_adc1.oscillator_strength[0], "bo")
plt.plot(1, xas_adc2.oscillator_strength[0], "bo")
plt.plot(2, xas_adc2x.oscillator_strength[0], "bo")
plt.plot(3, xas_adc3.oscillator_strength[0], "bo")
plt.xlim((-0.5, 3.5))
plt.ylabel("Absolute oscillator strength")
plt.xticks([0, 1, 2, 3], ("ADC(1)", "ADC(2)", "ADC(2)-x", "ADC(3/2)"))
plt.subplot(223)
plt.title("XES energy")
expt, rel = 527.10, 0.37
plt.plot(0, -au2ev * xes_adc1.excitation_energy[0] + rel - expt, "bo")
plt.plot(1, -au2ev * xes_adc2.excitation_energy[0] + rel - expt, "bo")
plt.plot(2, -au2ev * xes_adc2x.excitation_energy[0] + rel - expt, "bo")
plt.plot(3, -au2ev * xes_adc3.excitation_energy[0] + rel - expt, "bo")
plt.plot([-0.5, 3.5], [0, 0], "k--", zorder=0)
plt.xlim((-0.5, 3.5))
plt.ylabel("Error wrt experiment [eV]")
plt.xticks([0, 1, 2, 3], ("ADC(1)", "ADC(2)", "ADC(2)-x", "ADC(3/2)"))
plt.subplot(224)
plt.title("XES oscillator strength")
plt.plot(0, xes_adc1.oscillator_strength[0], "bo")
plt.plot(1, xes_adc2.oscillator_strength[0], "bo")
plt.plot(2, xes_adc2x.oscillator_strength[0], "bo")
plt.plot(3, xes_adc3.oscillator_strength[0], "bo")
plt.xlim((-0.5, 3.5))
plt.ylabel("Absolute oscillator strength")
plt.xticks([0, 1, 2, 3], ("ADC(1)", "ADC(2)", "ADC(2)-x", "ADC(3/2)"))
plt.tight_layout()
plt.show()
As can be seen, the smallest discrepancy for XAS is observed for CVS-ADC(2)-x, and for XES it is here for ADC(3/2). In general, it has been observed that CVS-ADC(2)-x performs best for XAS, and ADC(2) for XES (in terms of absolute energies - for relative features ADC(2)-x performs a bit better). As ADC(3/2) is correct in higher order of perturbation theory and performs well for valence excitations, it could be expected to also perform best for core properties. The fact that this is not the case has been discussed as being due to balancing in relaxation effects, which are highly influential for core properties and vary significantly between XAS and XES.
Furthermore, we see that the oscillator strengths vary greatly for XAS \(-\) in particular when comparing CVS-ADC(1) to higher orders of theory \(-\) but not very much for XES.
Including relaxation with DFT-based methods#
When using a \(\Delta\)KS approach, relaxation is explicitly accounted for, as discussed above. By contrast, TDDFT is a single-excitation theory which cannot properly account for relaxation (which requires doubly-excited configuration in a response theory framework), although it can be partially accounted for through some separate correction scheme. The error introduced by a lack of relaxation will furthermore be counteracted by the self-interaction error, as is discussed below.
Relativity#
Relativistic effects are significantly stronger for core than valence MOs, on account of the strong potential experienced by the core orbitals. These effects mainly influences calculated properties in two separate manners:
Scalar relativistic effects, which are always present and lead to a contraction (and thus increase in binding energy) of core orbitals. Higher lying orbitals (especially for \(l>1\)) can become decontracted due to increasing screening from contracted MOs, but this effect is typically much smaller than for, e.g., 1s orbitals
Spin-orbit coupling, which breaks degeneracies for MOs of \(l>0\) and is thus negligible for, e.g., the \(K\)- and \(L_1\)-edges (as the splitting for valence MOs is much smaller), but very important for, e.g., the \(L_{2,3}\)-edge
Scalar relativistic effects#
Including scalar relativistic effects is relatively straightforward, as a number of Hamiltonians are available which can include these effects in a 1-component framework. Furthermore, the effects are typically quite stable over the separate elements, and can thus often be considered as a common absolute off-set in energy. It should be noted that the (scalar) relativistic effects are technically not additive with electron correlation, such that a proper consideration should account for both simultaneously. In practice, this discrepancy is small and relativistic shifts from lower levels of theory are typically sufficient.
Spin-orbit coupling#
Including the spin-orbit effects is more complicated, and can either be
Included by using 4-component relativistic theory, where they do not need to explicitly addressed
Included in a non-relativistic approach through a perturbative scheme, or through some ad hoc correction
At the present stage, including spin-orbit effects is beyond the scope of this tutorial.
Basis set considerations#
The basis set requirements of X-ray spectrum calculations depend on which spectroscopy is considered
XPS and XES probe occupied states, and thus need a good description of those
XAS and RIXS probe excited states, and thus need an improved description of this region
In all cases the relaxation due to the creation of a core-hole needs to be accommodated, which yields requirements of reasonable flexibility of the core and inner valence region. This is not usually the case for standard basis sets, as they are typically constructed with valence properties in mind and thus have a minimal or close to minimal description of the core region. A number of approaches for improving such valence-focused basis sets have been developed by:
Augmenting the Dunning basis sets with core-polarizing functions, e.g. cc-pVnZ \(\rightarrow\) cc-pCVnZ
Adding extra flexibility by performing full or partial decontraction, such as
Decontracting 1s of the probed element (e.g. u6-311++G**, which is based on 6-311++G**)
Fully decontracting the basis set (e.g. un6-311++G**, which is based on 6-311++G**)
Using basis functions from the next element, as inspired by the \(Z+1\) approximation
As an illustration, we consider the IE of water with different basis sets and levels of theory
Note
Currently using pyscf – this will be updated.
Toggle for u6-311G**, un6-311G**, and 6-311G** (Z+1) basis sets.
from pyscf import gto
u6311gss = {'O': gto.basis.parse('''
O S
8588.500 1.000000
O S
1297.230 1.000000
O S
299.2960 1.000000
O S
87.37710 1.000000
O S
25.67890 1.000000
O S
3.740040 1.000000
O SP
42.11750 0.113889 0.0365114
9.628370 0.920811 0.237153
2.853320 -0.00327447 0.819702
O SP
0.905661 1.000000 1.000000
O SP
0.255611 1.000000 1.000000
O D
1.292 1.000000
'''), 'H': '6-311G**'}
un6311gss = {'O': gto.basis.parse('''
O S
8588.500 1.000000
O S
1297.230 1.000000
O S
299.2960 1.000000
O S
87.37710 1.000000
O S
25.67890 1.000000
O S
3.740040 1.000000
O SP
42.11750 1.000000 1.000000
O SP
9.628370 1.000000 1.000000
O SP
2.853320 1.000000 1.000000
O SP
0.905661 1.000000 1.000000
O SP
0.255611 1.000000 1.000000
O D
1.292 1.000000
'''), 'H': '6-311G**'}
z6311gss = {'O': gto.basis.parse('''
O S
8588.500 0.00189515
1297.230 0.0143859
299.2960 0.0707320
87.37710 0.2400010
25.67890 0.5947970
3.740040 0.2808020
O SP
42.11750 0.113889 0.0365114
9.628370 0.920811 0.237153
2.853320 -0.00327447 0.819702
O SP
0.905661 1.000000 1.000000
O SP
0.255611 1.000000 1.000000
O D
1.292 1.000000
O S
11427.10 0.00180093
1722.350 0.0137419
395.7460 0.0681334
115.1390 0.2333250
33.60260 0.5890860
4.919010 0.2995050
O SP
55.44410 0.114536 0.0354609
12.63230 0.920512 0.237451
3.717560 -0.00337804 0.820458
O SP
1.165450 1.000000 1.000000
O SP
0.321892 1.000000 1.000000
O D
1.750 1.000000
'''), 'H': '6-311G**'}
# Investigated basis sets
basis_sets = [
"6-311G**",
u6311gss,
un6311gss,
z6311gss,
"cc-pVDZ",
"cc-pCVDZ",
"cc-pVTZ",
"cc-pCVTZ",
"cc-pVQZ",
"cc-pCVQZ",
]
# Containers for IE calculated with four different delta calculations: HF, MP2, CCSD, and B3LYP
ip_hf, ip_mp2, ip_ccsd, ip_b3lyp, n_bas = [], [], [], [], []
for basis in basis_sets:
# Create pyscf mol object
mol = gto.Mole()
mol.atom = water_mol_str
mol.basis = basis
mol.build()
# Unrestricted SCF calculation of neutral
scfres = scf.UHF(mol)
scfres.kernel()
# Copy molecular orbitals and change population of 1s
mo0 = copy.deepcopy(scfres.mo_coeff)
occ0 = copy.deepcopy(scfres.mo_occ)
occ0[0][0] = 0.0
# Unrestricted HF calculation of core-hole and appending delta_HF IP
scfion = scf.UHF(mol)
scf.addons.mom_occ(scfion, mo0, occ0)
scfion.kernel()
ip_hf.append(au2ev * (scfion.energy_tot() - scfres.energy_tot()))
# CCSD calculations of neutral and core-hole and appending delta_CCSD IP
ccsd_res = cc.UCCSD(scfres).run()
ccsd_ion = cc.UCCSD(scfion).run(max_cycle=500)
ip_ccsd.append(au2ev * (ccsd_ion.e_tot - ccsd_res.e_tot))
# Appending delta_MP2 IP
ip_mp2.append(
au2ev * (ccsd_ion.e_hf + ccsd_ion.emp2 - (ccsd_res.e_hf + ccsd_res.emp2))
)
# Unrestricted KS-DFT calculation of neutral
scfres = scf.UKS(mol)
scfres.xc = "b3lyp"
scfres.kernel()
# Copy molecular orbitals and change population of 1s
mo0 = copy.deepcopy(scfres.mo_coeff)
occ0 = copy.deepcopy(scfres.mo_occ)
occ0[0][0] = 0.0
# Unrestricted KS-DFT calculation of core-hole and appending delta_DFT IP
scfion = scf.UKS(mol)
scf.addons.mom_occ(scfion, mo0, occ0)
scfion.xc = "b3lyp"
scfion.kernel()
ip_b3lyp.append(au2ev * (scfion.energy_tot() - scfres.energy_tot()))
# Append basis set size
n_bas.append(len(scfres.mo_occ[0]))
plt.figure(figsize=(10, 5))
# Plot IEs, with error as a function of basis set size
plt.plot(n_bas, ip_hf, "r*")
plt.plot(n_bas, ip_mp2, "bv")
plt.plot(n_bas, ip_ccsd, "d", color="orange")
plt.plot(n_bas, ip_b3lyp, "go")
plt.legend(("HF", "MP2", "CCSD", "B3LYP", "Expt", "Expt - 0.37 eV"))
# Experimental value as a dotted line, minus relativistic effect as dashed line
plt.plot([min(n_bas) - 5, max(n_bas) + 5], [539.9, 539.9], "k:")
plt.plot([min(n_bas) - 5, max(n_bas) + 5], [539.9 - 0.37, 539.9 - 0.37], "k--")
# Basis set label as x-ticks
basis_set_labels = [
"6-311G**",
"u6-311G**",
"un6-311G**",
"6-311G** (Z+1)",
"cc-pVDZ",
"cc-pCVDZ",
"cc-pVTZ",
"cc-pCVTZ",
"cc-pVQZ",
"cc-pCVQZ",
]
plt.xticks(n_bas, basis_set_labels, rotation=70, fontsize=10)
# Labels and setting x-interval
plt.ylabel("Ionization energy [eV]")
plt.xlim((min(n_bas) - 5, max(n_bas) + 5))
plt.tight_layout()
plt.show()
At the HF and KS-DFT levels of theory we see that some of the smaller basis sets have fortuitous error cancellations, such that both 6-311G** and cc-pVTZ yield results close to experimental values. However, augmenting these basis sets with more functions in the core region brings us away from experimental measurements (note that the calculations do not include relativistic effects, so the comparison would be toward experiment minus relativistic shift, i.e. the dashed line).
With MP2 and CCSD we note very similar results for the smaller basis sets, which then deviate significantly for cc-pVTZ and above. \(\Delta\)CCSD estimates using core-polarized cc-pVTZ and cc-pVQZ are well in line with experimental measurements. Augmenting the 6-311G** basis sets with a decontracted core region (u6-311G**) yields some improvement at a relatively low increase in computational cost, and further decontracting the full set (un6-311G**) or adding basis functions from \(Z+1\) (6-311G** (Z+1)) provides some additional improvement.
Self-interaction error in DFT#
For a single-electron systems the following equality should hold for the two-electron terms:
\[
J[\rho] + E_{xc} [\rho] = 0
\]
This cancellation is preserved within HF theory, but for any approximate functionals in KS-DFT the equality will no longer hold, resulting in the potentially significant errors due to spurious self-interactions. Reformulated, the Coulomb self-repulsion of each electron included in the Coulomb operator is exactly canceled by the nonlocal exchange self-attraction in Hartree-Fock, but this is no longer the case when the exchange operator is replaced by an approximate exchange functional.
As such, KS-DFT possess a self-interaction error (SIE), which shows a strong dependence on how compact the respective MOs are. This means that the self-interaction error is significantly more influential for core properties than for valence properties, and the tendency to decontract core orbitals due to the SIE has an opposite effect on transition energies as compared to relaxation effects.
Let us consider the ionization energy of water, as calculated with MO energies and \(\Delta\textrm{SCF}\) using two different exchange-correlation functionals with variable HF exchange:
Note
Currently using pyscf – this will be updated.
Note
Using MO energies for TDHF and TDDFT yields the same IE as when addressing core-transitions to extremely diffuse basis functions (due to the lack of relaxation), and is thus representative of the error for such XAS calculations.
# Create pyscf mol object
mol = gto.Mole()
mol.atom = water_mol_str
mol.basis = "6-31G"
mol.build()
# Investigated HF exchange and result containers
hf_exc = [0.0, 0.25, 0.50, 0.75, 1.0]
hf_blyp, hf_pbe = [[], []], [[], []]
def dft_delta(mol, xc):
# Neutral calculation
dft_res = scf.UKS(mol)
dft_res.xc = xc
dft_res.kernel()
# Core-hole calculation
mo0 = copy.deepcopy(dft_res.mo_coeff)
occ0 = copy.deepcopy(dft_res.mo_occ)
occ0[0][0] = 0.0
dft_ion = scf.UKS(mol)
dft_ion.xc = xc
scf.addons.mom_occ(dft_ion, mo0, occ0)
dft_ion.kernel()
return -au2ev * dft_res.mo_energy[0][0], au2ev * (
dft_ion.energy_tot() - dft_res.energy_tot()
)
for h_x in hf_exc:
# BxLYP (Slater exchange 0.08, except when HF i 1.00)
if h_x == 1.0:
s_x = 0.00
else:
s_x = 0.08
b_x = 1.00 - h_x - s_x
v_e, v_l = 0.19, 0.81
xc = f"{h_x:} * HF + {s_x:} * Slater + {b_x:} * B88, {v_l:} * LYP + {v_e:} * VWN"
E_mo, E_delta = dft_delta(mol, xc)
hf_blyp[0].append(E_mo)
hf_blyp[1].append(E_delta)
# PBEx
p_x = 1.0 - h_x
xc = f"{h_x:} * HF + {p_x:} * PBE, PBE"
E_mo, E_delta = dft_delta(mol, xc)
hf_pbe[0].append(E_mo)
hf_pbe[1].append(E_delta)
plt.figure(figsize=(6, 4))
# DFT ionization energies, including scalar relativistic shift
plt.plot(hf_exc, np.array(hf_blyp[0]) + 0.37, "bs--")
plt.plot(hf_exc, np.array(hf_blyp[1]) + 0.37, "ro--")
plt.plot(hf_exc, np.array(hf_pbe[0]) + 0.37, "d--", color="orange")
plt.plot(hf_exc, np.array(hf_pbe[1]) + 0.37, "g^--")
# Experimental value and legend
plt.plot([-0.1, 1.1], [539.9, 539.9], "k-")
plt.legend(
(r"BxLYP ($\Delta$SCF)", "BxLYP (MO)", r"PBEx ($\Delta$SCF)", "PBEx (MO)", "Expt")
)
plt.xlim((-0.025, 1.025))
plt.ylim((508, 562.0))
plt.xlabel("HF exchange [%]")
plt.ylabel("Ionization energy [eV]")
plt.tight_layout()
plt.show()
We see that the \(\Delta\)SCF errors are quite constant between the two base functionals and amounts of HF exchange, while the MO energies strongly scale with HF exchange, but not with the base functional. The total MO error is a function of two effects:
Lack of relaxation, which generally leads to an overestimation of IEs and core-excitation energies
Self-interaction, which by contrast leads to an underestimation of these energies
For a typical exchange-correlation functional (\(\sim\)20-25% HF exchange) the SIE thus dominates, and by tuning the (global) HF exchange to around 60% we achieve IE estimates in good agreement to experiment. We note that this is only acheieved by cancellation of the above two errors, and does not mean that we have an appropriate description of the core-excitation processes. Furthermore, a good exchange-correlation functional should possess good energies and densities, and focusing on only energies can push us away from such a goal. Nevertheless, a number of tailored functionals with good absolute energies have been constructed, tuning the HF exchange either in a global or range-separated manner. Note that the parameterization will have to depend on the spectroscopy, probed edge, and row of the periodic table, as the exact balance in relaxation terms and SIE varies.
Core-hole localization#
For \(\Delta\) SCF calculations (either for estimating IEs or as a initial state for XES), a core-hole is created at some atomic site. For many systems, this is unproblematic, but if chemically equivalent atoms are present, the MOs are delocalized over these sites. Performing a straightforward \(\Delta\)SCF calculation will then results in a delocalized core-hole, as illustrated below for ethene:
Note
Currently using pyscf – this will be updated.
ethene_mol_str = """
C0 0.6660048050 0.0000000000 -0.0000000000
C1 -0.6660048050 -0.0000000000 0.0000000000
H 1.2278735620 0.9228358077 -0.0000000000
H 1.2278735620 -0.9228358077 -0.0000000000
H -1.2278735620 0.9228358077 0.0000000000
H -1.2278735620 -0.9228358077 0.0000000000
"""
def Koopman_vs_delta(molecule, basis, ecp=None):
# Create pyscf mol object
mol = gto.Mole()
mol.atom = molecule
mol.basis = basis
if ecp:
mol.ecp = ecp
mol.build()
# Perform unrestricted SCF calculation
scf_gs = scf.UHF(mol)
scf_gs.kernel()
# Copy molecular orbitals
mo0 = copy.deepcopy(scf_gs.mo_coeff)
occ0 = copy.deepcopy(scf_gs.mo_occ)
# Create 1s core-hole by setting alpha_0 population to zero
occ0[0][0] = 0.0
# Perform unrestricted SCF calculation with MOM constraint
scf_ion = scf.UHF(mol)
scf.addons.mom_occ(scf_ion, mo0, occ0)
scf_ion.kernel()
# Return MO energy and deltaSCF
return -au2ev * scf_gs.mo_energy[0][0], au2ev * (
scf_ion.energy_tot() - scf_gs.energy_tot()
)
# All-electron calculation of IP
delta_all = Koopman_vs_delta(ethene_mol_str, "unc-6-31G")
# IE calculation with ECP on one carbon
delta_ecp = Koopman_vs_delta(ethene_mol_str, "unc-6-31G", {"C0": "stuttgart"})
plt.figure(figsize=(5, 3))
# IE estimates with all-electron (delocalized core-hole)
plt.plot([1, 2], [delta_all[0] + 0.11, delta_all[1] + 0.11], "ro")
# IE estimates with ECP (localized core-hole)
plt.plot([1, 2], [delta_ecp[0] + 0.11, delta_ecp[1] + 0.11], "bs")
# Experiment and figure settings
plt.plot([0.5, 2.5], [290.80, 290.80], "k--")
plt.ylabel("Ionization energy [eV]")
plt.xticks([1, 2], ("MO", r"$\Delta$SCF"))
plt.xlim((0.5, 2.5))
plt.tight_layout()
plt.show()
As can be seen, the errors from MO energies are very similar for the all-electron calculation (with a delocalized core-hole) and using ECP (delocalized core-hole). For the \(\Delta\)SCF calculation, however, only approximately half the relaxation energy is accounted for using a delocalized core-hole. Such a discrepancy for delocalized calculations of IEs has been noted previously, and it has been associated with missing correlation effects which are required to properly correct the delocalized calculation. Within a full CI scheme, delocalization will no longer be an issue (and it will capture the small shift in energy between the gerade and ungerade core-hole).
Moving from theory, in experiment the localizatio/delocalization of core-holes is primarily relevant for diatomic systems, as other compounds will possess vibrational effects which break the symmetry. For diatomic systems the localized/delocalized nature of the core-hole has been seen to depend on the details of the measurement, such that both can be probed [ref].
As such, for practical calculation we recommend that core-holes are localized for IE and XES calculations. For XAS it does not provide any issues for linear response methods (provided that both gerade and ungerade MOs are kept in the CVS space/equivalent), but for state-specific approaches this will again be an issue (e.g. STEX and TP-DFT).
Tailored CVS#
For large systems, it may become relevant to tailor the CVS space such that each chemically unique atom is probed in turn. While this requires explicit consideration of each set of unique MOs separately, it serves dual purposes which can make it worth it:
It lowers the dimensionality of the involved matrices, and thus decrease computational costs
The density-of-states decrease, which means that the same energy region can be resolved with a few states per unique MO, rather than having to converge a large number of eigenstates simultaneously
While this technically does not fulfill one of foundations on which the CVS approximation is built (the MOs are not energetically well-separated), the spatial separation means that it will typically work. As an example, we consider ethene (which has delocalized MOs) and vinylfluoride (which does not):
Note
Currently using pyscf – this will be updated.
vinyl_mol_str = """
C 0.000000 -0.246412 -1.271068
C 0.000000 0.457081 -0.154735
F 0.000000 -0.119195 1.052878
H 0.000000 0.272328 -2.210194
H 0.000000 -1.319906 -1.249847
H 0.000000 1.530323 -0.095954
"""
print("Ethene")
# Create pyscf mol object
mol = gto.Mole()
mol.atom = ethene_mol_str
mol.basis = "6-31G"
mol.build()
# Perform restricted SCF calculation
scf_gs = scf.RHF(mol)
scf_gs.kernel()
# Perform CVS-ADC calculations
ethene_adc1_0 = adcc.cvs_adc1(scf_gs, n_singlets=4, core_orbitals=[0])
ethene_adc1_1 = adcc.cvs_adc1(scf_gs, n_singlets=4, core_orbitals=[1])
ethene_adc1_01 = adcc.cvs_adc1(scf_gs, n_singlets=4, core_orbitals=[0, 1])
ethene_adc2_0 = adcc.cvs_adc2(scf_gs, n_singlets=4, core_orbitals=[0])
ethene_adc2_1 = adcc.cvs_adc2(scf_gs, n_singlets=4, core_orbitals=[1])
ethene_adc2_01 = adcc.cvs_adc2(scf_gs, n_singlets=4, core_orbitals=[0, 1])
print("Vinylfluoride")
# Create pyscf mol object
mol = gto.Mole()
mol.atom = vinyl_mol_str
mol.basis = "6-31G"
mol.build()
# Perform restricted SCF calculation
scf_gs = scf.RHF(mol)
scf_gs.kernel()
# Perform CVS-ADC calculations
vinyl_adc1_1 = adcc.cvs_adc1(scf_gs, n_singlets=4, core_orbitals=[1])
vinyl_adc1_2 = adcc.cvs_adc1(scf_gs, n_singlets=4, core_orbitals=[2])
vinyl_adc1_12 = adcc.cvs_adc1(scf_gs, n_singlets=4, core_orbitals=[0, 1, 2])
vinyl_adc2_1 = adcc.cvs_adc2(scf_gs, n_singlets=4, core_orbitals=[1])
vinyl_adc2_2 = adcc.cvs_adc2(scf_gs, n_singlets=4, core_orbitals=[2])
vinyl_adc2_12 = adcc.cvs_adc2(scf_gs, n_singlets=4, core_orbitals=[0, 1, 2])
plt.figure(figsize=(10, 6))
# Ethene with CVS-ADC(1)
plt.subplot(221)
plt.title("Ethene")
ethene_adc1_0.plot_spectrum(label="MO #0")
ethene_adc1_1.plot_spectrum(label="MO #1")
ethene_adc1_01.plot_spectrum(label="MOs #0-1")
plt.legend()
plt.ylabel("CVS-ADC(1)")
# Vinylfluoride with CVS-ADC(1)
plt.subplot(222)
plt.title("Vinylfluoride")
vinyl_adc1_1.plot_spectrum(label="MO #1")
vinyl_adc1_2.plot_spectrum(label="MO #2")
vinyl_adc1_12.plot_spectrum(label="MO #1-2")
plt.legend()
# Ethene with CVS-ADC(2)
plt.subplot(223)
ethene_adc2_0.plot_spectrum()
ethene_adc2_1.plot_spectrum()
ethene_adc2_01.plot_spectrum()
plt.ylabel("CVS-ADC(2)")
# Vinylfluoride with CVS-ADC(2)
plt.subplot(224)
vinyl_adc2_1.plot_spectrum()
vinyl_adc2_2.plot_spectrum()
vinyl_adc2_12.plot_spectrum()
plt.tight_layout()
plt.show()
We see that considering each MO in turn works well for vinylfluoride, where the two carbon 1s are localized, but not for ethene, where they are delocalized. Including or not including fluorine here makes little difference, as that MO is both energetically and spatially well separated from the carbon 1s.
Note that the delocalization might not be immediatelly apparent, as just visually looking at the molecule and concluding which atoms are unique might not be sufficient. Care should be taken for larger systems, and explicitly looking at the MOs is advised. Alternatively, using ECPs to localize the core-hole and then restricting the CVS space accordingly will avoid this issue.
Post-HF on a non-Aufbau reference#
Note
Include a discussion on the potential issues in using post-HF methods for a non-Aufbau reference state, as can be seen by noting the MP2 energy denominator (and potential singularities, and discusses here)
Include explicit example:
Go over all permutations (aa, ab, bb), saving the highest MO index which yields denominators below 0.1 au. Just have a list of virtual indices, adding when an index is not already found there. Do this in one shot, instead of saving one virtual at a time.
Compare this to the scheme in adcc, noting that the present (simpler) scheme is likely just as useful - despite not ordering indices by how problematic they are.
Use this to calculate the ADC(2)/cc-pCVQZ spectra of ammonia, with and without frozen virtuals.
Spurious valence mixing in XAS#
Within a damped response theory framework or when performing explicit real-time propagation, a CVS-like scheme which separates core-transitions from the valence-continuum is usually not performed. If such calculations are run with an atom-centered basis set (as most are), this can then lead to spurious mixing with valence-excited states. What happens is that resonances in the valence-continuum occur close to core-excitations, leading to unphysical mixing which affects excitation energies and (more significantly) intensities. These issues occur both for methods featuring only single-excited configurations (e.g. TDDFT) and higher-excited configurations (e.g. ADC) and need to be avoided.
These issues have been observed for, e.g., \(L_{2,3}\)-edge of silicon [FBN16, KKG+15], and are usually more common at lower energies. They can be identified by studying the amplitudes and the \(t^2\) values for post-HF methods, and can be avoided by chosing appropriate basis sets, freezing certain virtual orbitals, or by re-introducing the CVS approximation (or some other flavour) within the CPP/RT framework. The latter approach is recommended at least for CPP-ADC, as converging the response vectors has otherwise been seen to be difficult [RRH+21].