Reduced particle densities

Consider an \(N\)-electron system in a state represented by a general state vector that can be expressed as a linear combination of Slater determinants

\[ | \Psi \rangle = \sum_n c_n | \Phi_n \rangle \]

The one- and two-particle particle reduced densities can be evaluated as expectation values of one- and two-particle operators, respectively, using the expressions for matrix elements. The resulting formulas will be expressions involving products of molecular orbitals from which we can identify one- and two-particle density matrices.

As an illustration, we will determine the one- and two-particle densities along the internuclear axis of carbon monoxide at the level of Hartree–Fock theory.

import matplotlib.pyplot as plt
import numpy as np
import veloxchem as vlx

mol_str = """
C        0.00000000    0.00000000    0.00000000
O        0.00000000    0.00000000    2.70000000
"""
molecule = vlx.Molecule.read_molecule_string(mol_str, units="au")
basis = vlx.MolecularBasis.read(molecule, "cc-pVDZ", ostream=None)

scf_drv = vlx.ScfRestrictedDriver()
scf_drv.ostream.mute()

scf_results = scf_drv.compute(molecule, basis)

C = scf_results["C_alpha"]
D = scf_results["D_alpha"] + scf_results["D_beta"]

norb = basis.get_dimensions_of_basis()
nocc = molecule.number_of_alpha_electrons()

print("Number of contracted basis functions:", norb)
print("Number of doubly occupied molecular orbitals:", nocc)

Number of contracted basis functions: 28
Number of doubly occupied molecular orbitals: 7

One-particle density

Probabilistic interpretation

The probability density of finding any one electron in an infinitesimal volume element at position \(\mathbf{r}\) regardless of the positions of other electrons is equal to

\[ n(\mathbf{r}) = N \int \cdots \int \Psi^\dagger(\mathbf{r}, \mathbf{r}_2, \ldots, \mathbf{r}_N) \Psi(\mathbf{r}, \mathbf{r}_2, \ldots, \mathbf{r}_N) \, \mathrm{d}^3 \mathbf{r}_2 \cdots \mathrm{d}^3\mathbf{r}_N \]

Expectation values

For a scalar one-electron operator in coordinate basis taking the form

\[ \hat{\Omega} = \sum_{i=1}^N \omega(\mathbf{r}_i) \]

the expectation value relates to the one-particle density according to

\[\begin{align*} \langle \hat{\Omega} \rangle & = \int \cdots \int \Psi^\dagger(\mathbf{r}_1, \mathbf{r}_2, \ldots, \mathbf{r}_N) \, \hat{\Omega} \, \Psi(\mathbf{r}_1, \mathbf{r}_2, \ldots, \mathbf{r}_N) \, \mathrm{d}^3 \mathbf{r}_1 \mathrm{d}^3 \mathbf{r}_2 \cdots \mathrm{d}^3\mathbf{r}_N \\ & = N \int \omega(\mathbf{r}) \Big[ \int \cdots \int \Psi^\dagger(\mathbf{r}, \mathbf{r}_2, \ldots, \mathbf{r}_N) \Psi(\mathbf{r}, \mathbf{r}_2, \ldots, \mathbf{r}_N) \, \mathrm{d}^3 \mathbf{r}_2 \cdots \mathrm{d}^3\mathbf{r}_N \Big] \mathrm{d}^3 \mathbf{r} \\ & = \int \omega(\mathbf{r}) \, n(\mathbf{r}) \, \mathrm{d}^3 \mathbf{r} \end{align*}\]

One-particle density operator

The one-particle density can be written as an expectation of a one-electron operator according to

\[ n(\mathbf{r}) = \langle \Psi | \hat{n}(\mathbf{r}) | \Psi \rangle \]

where

\[ \hat{n}(\mathbf{r}) = \sum_{i=1}^N \delta(\mathbf{r} - \mathbf{r}_i) \]

and \(\delta(\mathbf{r} - \mathbf{r}_i)\) is the Dirac delta function.

After evaluation of this expectation value, the one-particle density matrix, \(D\), is identified from the expression

\[ n(\mathbf{r}) \equiv \sum_{p,q} D_{pq} \, \psi_p^\dagger(\mathbf{r}) \psi_q(\mathbf{r}) \]

For a state represented by a single Slater determinant, the one-electron density becomes

\[ n(\mathbf{r}) = \sum_{i=1}^N |\psi_i(\mathbf{r})|^2 \]

where the summation run over the \(N\) occupied spin orbitals. Consequently, the density matrix is in this case equal to the identity matrix in the occupied–occupied block and zero elsewhere.

For a restricted closed-shell state, we get

\[ n(\mathbf{r}) = 2 \sum_{i}^\mathrm{occ} |\phi_i(\mathbf{r})|^2 = \sum_{p,q} D^\mathrm{MO}_{pq} \, \phi_p^*(\mathbf{r}) \phi_q(\mathbf{r}) \]

where the summations runs over molecular orbitals (MOs) and the density matrix in the MO basis equals

\[\begin{split} \mathbf{D}^\mathrm{MO} = \begin{pmatrix} 2 & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & 2 & 0 & \cdots & 0 \\ 0 & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & 0 & \cdots & 0 \\ \end{pmatrix} \end{split}\]

In the atomic orbital (AO) basis, we have

\[ n(\mathbf{r}) = \sum_{\alpha, \beta} D_{\alpha\beta}^\mathrm{AO} \, \chi_\alpha^\ast(\mathbf{r}) \chi_\beta(\mathbf{r}) \]

where

\[ D_{\alpha\beta}^\mathrm{AO} = 2 \sum_i^\mathrm{occ} c^*_{\alpha i} c_{\beta i} \]

or, equivalently,

\[ \mathbf{D}^\mathrm{AO} = \mathbf{C}^* \mathbf{D}^\mathrm{MO} \mathbf{C}^T \]

D_mo = np.zeros((norb, norb))

for i in range(nocc):
    D_mo[i, i] = 2.0

D_ao = np.einsum("ap, pq, bq -> ab", C, D_mo, C)

Test MO to AO transformation against the reference density matrix from VeloxChem.

np.testing.assert_allclose(D_ao, D, atol=1e-12)

Illustration

The one-particle density is available in VeloxChem by means of the VisualizationDriver class. As indicated by the string argument “alpha” in the get_density method, the \(\alpha\)- and \(\beta\)-spin densities can be determined individually, referring to the relation

\[ n(\mathbf{r}) = n^\alpha(\mathbf{r}) + n^\beta(\mathbf{r}) \]

For a closed shell system, the two spin densities are equal and thus equal to half the total one-particle density.

Considering the one-particle density of CO, as calculated along the line intersecting both atoms:

vis_drv = vlx.VisualizationDriver()

# list of coordinates in units of Bohr
n = 2000
coords = np.zeros((n, 3))
z = np.linspace(-1, 4, n)
coords[:, 2] = z
one_part_den = vis_drv.get_density(coords, molecule, basis, scf_drv.density, "alpha")

fig = plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.plot(z, one_part_den, lw=2, label=r"$n^\alpha(\mathbf{r})$")
plt.setp(plt.gca(), xlim=(-1, 4))
plt.legend()
plt.xlabel(r"Internuclear axis coordinate (Bohr)")
plt.ylabel(r"One-particle density (a.u.)")

plt.subplot(1, 2, 2)
plt.plot(z, one_part_den, lw=2, label=r"$n^\alpha(\mathbf{r})$")
plt.plot(z, one_part_den, "ko")
plt.grid(True)
plt.setp(plt.gca(), xlim=(-0.05, 0.05), ylim=(50, 62))
plt.legend()
plt.xlabel(r"Internuclear axis coordinate (Bohr)")
plt.ylabel(r"One-particle density (a.u.)")

plt.show()

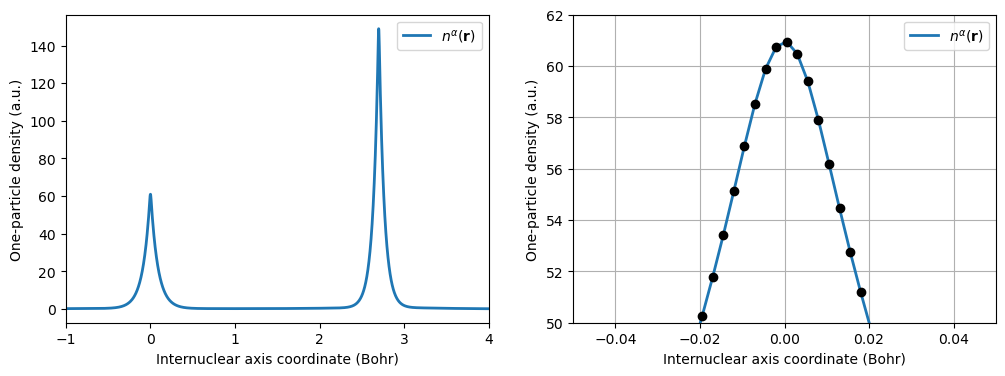
The right figure panel is an enlargement of the one-particle density in the region of the carbon nucleus, illustrating the fact that \(n(\mathbf{r})\) displays a cusp at any given nuclear position.

Two-particle density

Probabilistic interpretation

The probability density of finding any two electrons in separate infinitesimal volume elements at positions \(\mathbf{r}_1\) and \(\mathbf{r}_2\) regardless of the positions of other electrons is equal to

\[ n(\mathbf{r}_1, \mathbf{r}_2) = N (N-1) \int \cdots \int \Psi^\dagger(\mathbf{r}_1, \mathbf{r}_2, \mathbf{r}_3, \ldots, \mathbf{r}_N) \Psi(\mathbf{r}_1, \mathbf{r}_2, \mathbf{r}_3, \ldots, \mathbf{r}_N) \, \mathrm{d}^3 \mathbf{r}_3 \cdots \mathrm{d}^3\mathbf{r}_N \]

Expectation values

For a scalar two-electron operator in coordinate basis taking the form

\[ \hat{\Omega} = \sum_{j>i}^N \omega(\mathbf{r}_i, \mathbf{r}_j) \]

the expectation value relates to the one-particle density according to

\[\begin{align*} \langle \hat{\Omega} \rangle & = \int \cdots \int \Psi^\dagger(\mathbf{r}_1, \ldots, \mathbf{r}_N) \, \hat{\Omega} \, \Psi(\mathbf{r}_1, \ldots, \mathbf{r}_N) \, \mathrm{d}^3 \mathbf{r}_1 \cdots \mathrm{d}^3\mathbf{r}_N \\ & = \frac{N (N-1)}{2} \int \int \omega(\mathbf{r}_1, \mathbf{r}_2) \Big[ \int \cdots \int \Psi^\dagger(\mathbf{r}_1, \ldots, \mathbf{r}_N) \Psi(\mathbf{r}_1, \ldots, \mathbf{r}_N) \, \mathrm{d}^3 \mathbf{r}_3 \cdots \mathrm{d}^3\mathbf{r}_N \Big] \mathrm{d}^3 \mathbf{r}_1 \mathrm{d}^3 \mathbf{r}_2 \\ & = \frac{1}{2} \int \omega(\mathbf{r}_1, \mathbf{r}_2) \, n(\mathbf{r}_1, \mathbf{r}_2) \, \mathrm{d}^3 \mathbf{r}_1 \mathrm{d}^3 \mathbf{r}_2 \end{align*}\]

Two-particle density operator

The two-particle density can be written as an expectation of a two-electron operator according to

\[ n(\mathbf{r}, \mathbf{r}') = \langle \Psi | \hat{n}(\mathbf{r}, \mathbf{r}') | \Psi \rangle \]

with

\[ \hat{n}(\mathbf{r}, \mathbf{r}') = \sum_{i=1}^N \sum_{j>i}^N \left[ \delta(\mathbf{r} - \mathbf{r}_i) \delta(\mathbf{r}' - \mathbf{r}_j) + \delta(\mathbf{r} - \mathbf{r}_j) \delta(\mathbf{r}' - \mathbf{r}_i) \right] \]

After evaluation of this expectation value, the two-particle density matrix, \(D\), is identified from the expression

\[ n(\mathbf{r}, \mathbf{r}') \equiv \sum_{p, q, r, s} \psi_p^\dagger(\mathbf{r}) \psi_q(\mathbf{r}) D_{pqrs} \psi_r^\dagger(\mathbf{r}') \psi_s(\mathbf{r}') \]

For a state represented by a single Slater determinant, the two-electron density becomes

\[ n(\mathbf{r}, \mathbf{r}') = \sum_{i=1}^N \sum_{j=1}^N \left[\rule{0pt}{12pt} |\psi_i(\mathbf{r})|^2 |\psi_j(\mathbf{r}')|^2 - \psi_i^\dagger(\mathbf{r}) \psi_j^\dagger(\mathbf{r}') \psi_j(\mathbf{r}) \psi_i(\mathbf{r}') \right] \]

where the summations run over the \(N\) occupied spin orbitals.

Illustration

As indicated by the string arguments “alpha” and “beta” in the get_two_particle_density method, the spin densities can be determined individually, referring to the relation

\[ n(\mathbf{r}_1, \mathbf{r}_2) = n^{\alpha\alpha}(\mathbf{r}_1, \mathbf{r}_2) + n^{\alpha\beta}(\mathbf{r}_1, \mathbf{r}_2) + n^{\beta\alpha}(\mathbf{r}_1, \mathbf{r}_2) + n^{\beta\beta}(\mathbf{r}_1, \mathbf{r}_2) \]

For a closed shell system, we have

\[\begin{align*} n^{\alpha\alpha}(\mathbf{r}_1, \mathbf{r}_2) & = n^{\beta\beta}(\mathbf{r}_1, \mathbf{r}_2) \\ n^{\alpha\beta}(\mathbf{r}_1, \mathbf{r}_2) & = n^{\beta\alpha}(\mathbf{r}_1, \mathbf{r}_2) \end{align*}\]

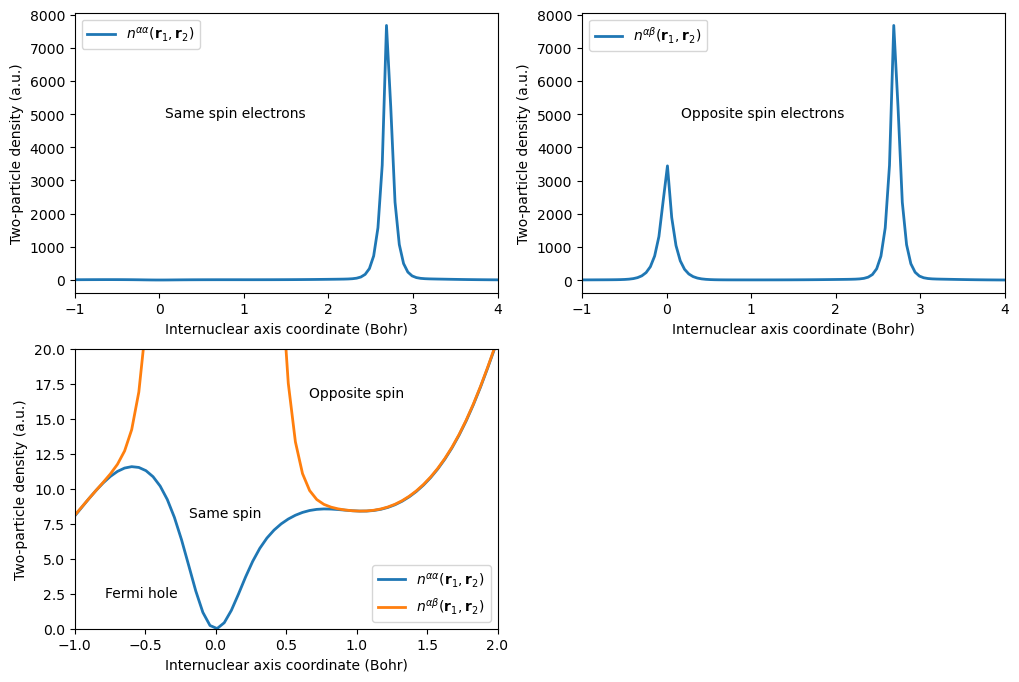
We will determine the two-particle density for electron 1 being positioned at the carbon nucleus and electron 2 being positioned along the internuclear axis.

n = 100
origin = np.zeros((n, 3))
coords = np.zeros((n, 3))
z = np.linspace(-1, 4, n)
coords[:, 2] = z

two_part_den_aa = vis_drv.get_two_particle_density(
    origin, coords, molecule, basis, scf_drv.density, "alpha", "alpha"
)
two_part_den_ab = vis_drv.get_two_particle_density(
    origin, coords, molecule, basis, scf_drv.density, "alpha", "beta"
)

fig = plt.figure(figsize=(12, 8))
plt.subplot(2, 2, 1)
plt.plot(
    z, two_part_den_aa, lw=2, label=r"$n^{\alpha\alpha}(\mathbf{r}_1, \mathbf{r}_2)$"
)
plt.setp(plt.gca(), xlim=(-1, 4))
plt.legend()
plt.figtext(0.2, 0.75, r"Same spin electrons")
plt.xlabel(r"Internuclear axis coordinate (Bohr)")
plt.ylabel(r"Two-particle density (a.u.)")

plt.subplot(2, 2, 3)
plt.plot(
    z, two_part_den_aa, lw=2, label=r"$n^{\alpha\alpha}(\mathbf{r}_1, \mathbf{r}_2)$"
)
plt.plot(
    z, two_part_den_ab, lw=2, label=r"$n^{\alpha\beta}(\mathbf{r}_1, \mathbf{r}_2)$"
)
plt.setp(plt.gca(), xlim=(-1, 2), ylim=(0, 20))
plt.legend()
plt.figtext(0.22, 0.25, r"Same spin")
plt.figtext(0.15, 0.15, r"Fermi hole")
plt.figtext(0.32, 0.4, r"Opposite spin ")
plt.xlabel(r"Internuclear axis coordinate (Bohr)")
plt.ylabel(r"Two-particle density (a.u.)")

plt.subplot(2, 2, 2)
plt.plot(
    z, two_part_den_ab, lw=2, label=r"$n^{\alpha\beta}(\mathbf{r}_1, \mathbf{r}_2)$"
)
plt.setp(plt.gca(), xlim=(-1, 4))
plt.legend()
plt.figtext(0.63, 0.75, r"Opposite spin electrons")
plt.xlabel(r"Internuclear axis coordinate (Bohr)")
plt.ylabel(r"Two-particle density (a.u.)")

plt.show()