Selection rules

Selection rules#

Spectrum intensities are proportional to the square modulus of transition moments

\[ \sigma_{f\leftarrow i} \propto \left| \langle \Psi_f | \hat{\Omega} | \Psi_i \rangle \right|^2 \]

where the quantum mechanical operator \(\hat{\Omega}\) provides the coupling between the molecular system and the external electromagnetic fields. Examples of such coupling operators are the electric and magnetic dipole moment operators and the electric quadrupole moment operator.

The study of the symmetry groups of molecular systems has immediate and powerful practical consequences. Specifically, we can predict when transition moments (and therefore also spectrum intensities) are zero due to reasons of symmetry. Such analyses are based on the result that an integral such as the transition moment is nonzero if and only if the direct product of the irreducible representations involved is equal to the all-symmetric representation

\[ \Gamma(\Psi_f) \otimes \Gamma(\hat{\Omega}) \otimes \Gamma(\Psi_i) = \Gamma(\hat{I}) \]

Let us view a simple and concrete example how symmetry can be used to determine a few selection rules for electric- and magnetic-field induced transitions of a \(\pi\)-stacked system. We will use the ethylene dimer with a separation distance of 4 Å as an illustration.

3Dmol.js failed to load for some reason. Please check your browser console for error messages.

This system belongs to the \(D_{2h}\) point group with eight irreducible representations presented in the character table.

The ground (or initial) state is closed-shell in nature and we thus have

\[ \Gamma(\Psi_i) = A_g \]

We start by performing an SCF optimization of this ground state at the DFT level of theory using the BHANDHLYP functional to view the molecular orbitals (MOs) and, more, specifically, their symmetry character.

import veloxchem as vlx

scf_drv = vlx.ScfRestrictedDriver()
scf_drv.ostream.mute()

molecule = vlx.Molecule.read_xyz_string(dimer_xyz)
basis = vlx.MolecularBasis.read(molecule, "6-31g", ostream=None)

scf_drv.xcfun = "bhandhlyp"
scf_results = scf_drv.compute(molecule, basis)

viewer = vlx.OrbitalViewer()
viewer.plot(molecule, basis, scf_drv.mol_orbs)

While one can change the selection of MO in the pull-down menu in a Jupyter notebook, this HTML page is static. For this reason, the \(\pi\)-conjugated frontier orbitals have been collected in the figure below, which represents a slight variation of an illustration found in Ref. [NL14].

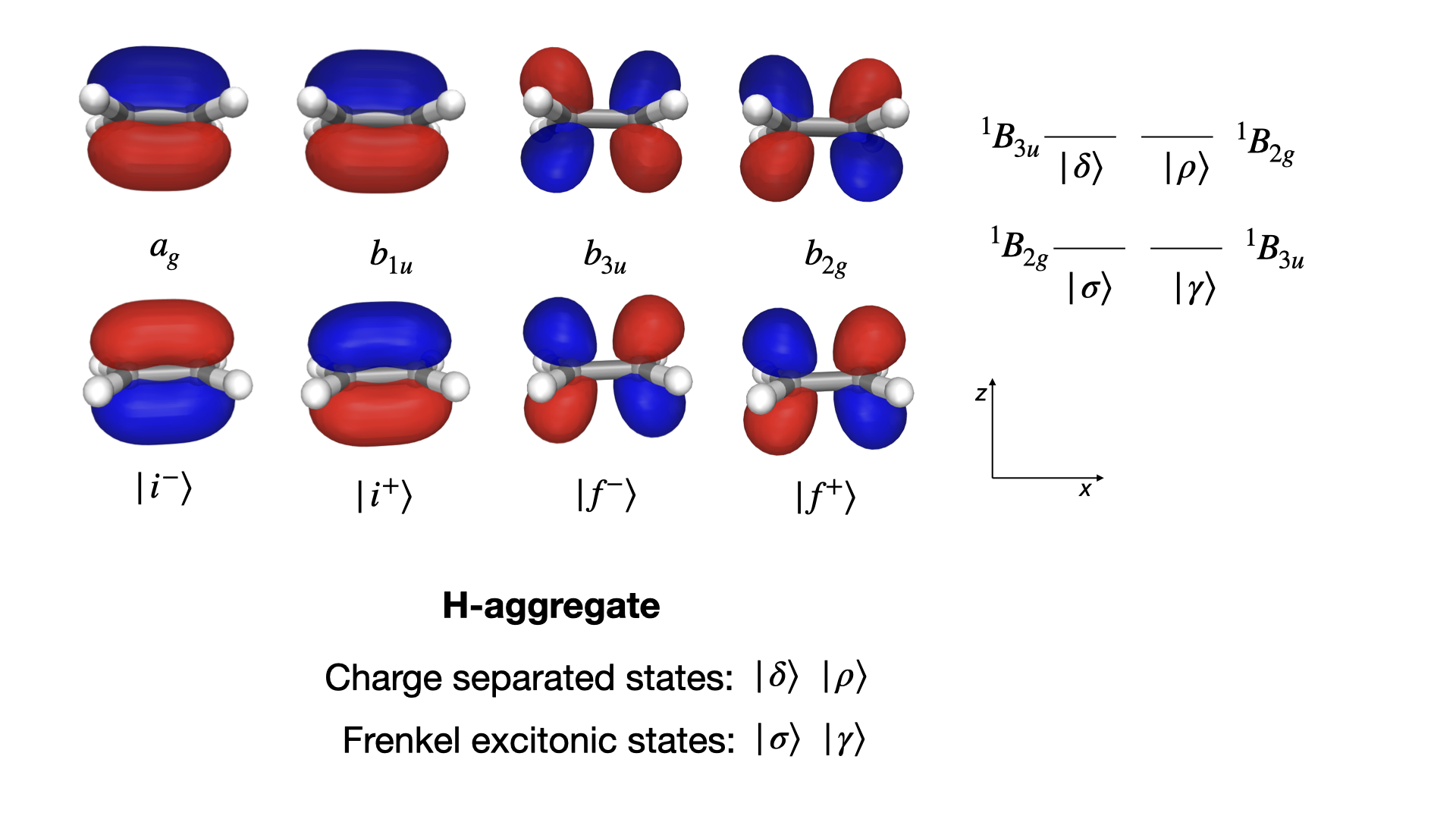
H-aggregate

The MOs of supramolecular system can be considered as linear combinations of the \(\pi\)- and \(\pi^*\)-orbitals of the monomers with main characters as follows

\[\begin{align*} |i^-\rangle = \pi_1 - \pi_2 \\ |i^+\rangle = \pi_1 + \pi_2 \\ |f^-\rangle = \pi_1^* - \pi_2^* \\ |f^+\rangle = \pi_1^* + \pi_2^* \\ \end{align*}\]

where, respectively, \(i\) and \(f\) denote initial and final electronic states in the excitation process. With two initial and two final orbitals, we can form four excited states.

The symmetries of these MOs are straightforwardly identified from the character table and given in the figure with the conventional use of small letters for denoting symmetries of MOs and capital letters for symmetries of multi-electron wave functions.

State \(| \sigma\rangle\) is lowest in energy and (primarily) associated with a HOMO–LUMO excitation giving rise to a \({}^1B_{2g}\) state. This state is electric-dipole forbidden. However, it couples to the ground state by means of the magnetic-dipole operator \(\hat{m}_y\) that transforms as the rotation \(R_y\) in the character table.
State \(| \gamma\rangle\) follows next in energy and is (primarily) associated with a mix of (HOMO-1)–LUMO and HOMO–(LUMO+1) excitations giving rise to a \({}^1B_{3u}\) state. This state is magnetic-dipole forbidden. However, it couples to the ground state by means of the electric-dipole operator \(\hat{\mu}_x\) that transforms as the coordinate \(x\) in the character table.

lreig_drv = vlx.LinearResponseEigenSolver()
lreig_drv.ostream.mute()

lreig_drv.nstates = 4

lreig_results = lreig_drv.compute(molecule, basis, scf_results)

print(f"   {'E (eV)':8s}{'mu_x':8s}{'mu_y':8s}{'mu_z':8s}{'m_x':8s}{'m_y':8s}{'m_z':8s}{'f':8s}{'R':8s}")
print(72 * "-")

for E, e, m, f, R in zip(
    lreig_results["eigenvalues"],
    lreig_results["electric_transition_dipoles"],
    lreig_results["magnetic_transition_dipoles"],
    lreig_results["oscillator_strengths"],
    lreig_results["rotatory_strengths"],
):
    print(
        f"{E*27.2114:8.4f}{e[0]:8.4f}{e[1]:8.4f}{e[2]:8.4f}{m[0]:8.4f}{m[1]:8.4f}{m[2]:8.4f}{f:8.4f}{R:8.4f}"
    )

   E (eV)  mu_x    mu_y    mu_z    m_x     m_y     m_z     f       R       
------------------------------------------------------------------------
  7.5915  0.0000 -0.0000  0.0000  0.0000 -0.9272  0.0000  0.0000  0.0000
  8.2471  1.6703  0.0000  0.0000  0.0000  0.0000  0.0000  0.5637  0.0000
  8.4311  0.9185  0.0000 -0.0000 -0.0000 -0.0000 -0.0000  0.1743 -0.0000
  8.7460 -0.0000  0.0000 -0.0000  0.0000 -0.4909  0.0000  0.0000  0.0000

So a symmetry analysis allows us to understand the UV/vis absorption and circular dichroism (CD) spectra of H-stacked aggregates. In absorption spectroscopy, the \(\pi\pi^*\)-band of the monomer becomes split into a lower dark band and an upper bright band that acquires the intensity from the two monomers. In CD spectroscopy, none of the bands gives rise to a signal. However, in a twisted supramolecular configuration, the symmetry of the system becomes lower and a bisignate excitonic band is formed from the two Frenkel states [NL14].