Intermediate state representation#
Derivation via intermediate states#
As the name suggest, the intermediate state representation (ISR) approach consists of constructing the ADC matrix with the help of intermediate states \(\ket{\tilde{\Psi}_I}\), obtained by applying excitation operators to the ground state \(\ket{0}\). In second quantization, the excitation operator is written as
where the indices \(a,b...\) refer to unoccupied orbitals, while \(i,j...\) represent occupied orbitals [MS96, Sch91, ST04]. Schematic representations of single and double excitations, which are the only two excitation classes that are needed for ADC up to third order in perturbation theory, are depicted, with (a) single excitations, (b) double excitations, and (c) the structure of the ADC(2) matrix. The numbers in parenthesis indicate the highest order of perturbation theory used to describe each particular block.
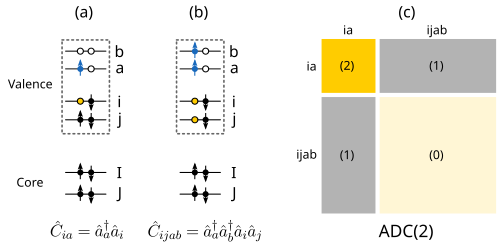
The intermediate states \(\ket{\tilde{\Psi}_I}\) are obtained by first applying \(\hat{C}_I\) to the many-body ground state
and then performing a Gram–Schmidt orthogonalization procedure with respect to lower excitation classes (including the ground state) to obtain precursor states \(\ket{\Psi_I^{\#}}\), which can then be orthonormalized symmetrically according to [Wen16]
where \(S_{IJ}=\braket{\Psi_I^{\#}|\Psi_J^{\#}}\) are overlap integrals of the precursor states.
The elements of the ADC matrix \(\mathbf{M}\) are obtained as matrix elements of the shifted Hamiltonian in the basis of the intermediate states
where \(E_0\) is the ground-state energy. This representation of the (shifted) Hamiltonian leads to a Hermitian eigenvalue equation
the solution of which yields vertical excitation energies (\(\omega_n = E_n - E_0\)) as eigenvalues, collected in the diagonal matrix \(\mathbf{\Omega}\), and the corresponding excitation vectors as eigenvectors \(\mathbf{Y}_n\), collected in the columns of \(\mathbf{Y}\).
Having obtained an expression for the ADC matrix, we return to the series expansion of the polarization propagator. In the same way as the propagator is expanded in series, also the matrix elements can be written in terms of orders of perturbation [Wen16]
where \(k\) and \(m\) are the orders of perturbation theory used for the overlap matrices \(S_{IK}\) and \(S_{LJ}\), \(l\) is the order used for the matrix elements of the shifted Hamiltonian in the basis of precursor states, and the sum \(k + l + m = n\) represents the order of the contribution to the ADC matrix \(\mathbf{M}\). In order to get all contributions of a given order \(n\), one needs to sum \(k,l,m\) over all terms for which \(k+l+m = n\).
The effective transition amplitudes \(\mathbf{f}\) can analogously be obtained in the ISR via
and the transition density matrices or transition amplitudes \(\mathbf{x}\) by contracting with the eigenvectors, \(\mathbf{x} = \mathbf{Y}^\dagger \mathbf{f}\). Note that since \(\mathbf{f}\) is a transition amplitude and not an expectation value, it is not symmetric: \(f_{I,pq} \neq f_{I,qp}\).
Structure of the ADC matrix#
As is shown here, the ADC eigenvalue equation in the space of single (S) and double (D) excitations can be written as
where the subscript denote the corresponding subblocks of the ADC matrix and \(\mathbf{X}_{\text{S}}\) is the singles part of the eigenvector. From this, the order structure of the ADC matrix can be explained as follows. The leading contributions of \(\mathbf{M}_{\text{SS}}\) and \(\mathbf{M}_{\text{DD}}\), and thus also of \((\omega \mathbf{1} - \mathbf{M}_{\text{DD}})^{-1}\), are of zeroth order, whereas the leading contributions of \(\mathbf{M}_{\text{SD}}\) and \(\mathbf{M}_{\text{DS}}\) are of first order. Hence, if excited states dominated by single excitations are desired through, say, second order, then \(\mathbf{M}_{\text{eff}}\) needs to be correct through this order, meaning that \(\mathbf{M}_{\text{SS}}\) needs to be correct through second order, \(\mathbf{M}_{\text{SD}}\) and \(\mathbf{M}_{\text{DS}}\) need to be correct through first order, whereas \(\mathbf{M}_{\text{DD}}\) only needs to be correct through zeroth order. Expanding \(\mathbf{M}_{\text{DD}}\) through first order would lead to a third-order term since the coupling blocks are at least of first order. Equivalently, expanding the coupling blocks through second order would lead to third-order terms, which are neglected in a second-order scheme. A consistent third-order method requires each block one order higher in perturbation theory, i.e. the singles-singles block through third oder, the coupling blocks through second order and the doubles-doubles block through first order. These findings are depicted schematically below for ADC(\(n\)) schemes up to third order. ADC(2)-x represents an ad hoc extension of ADC(2), where the first-order terms in the doubles-doubles block from ADC(3) are taken into account in order to improve the description of doubly excited states. However, this generally leads to an imbalanced description of singly and doubly excited states [DW15]. The structure of the ADC(\(n\)) matrix at different orders \(n\) is illustrated below. The numbers indicate the orders of perturbation theory used to expand the corresponding block.
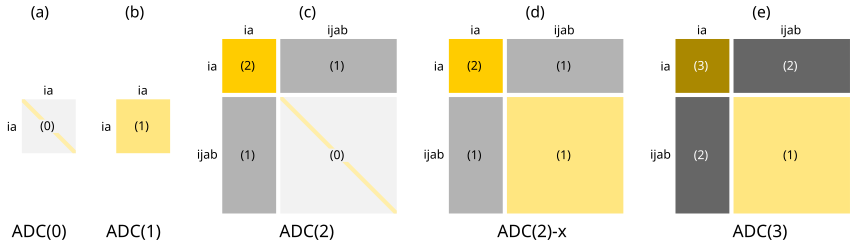
Explicit expressions for ADC(2)#
Using above expansion of \(M_{IJ}\) in combination with specific classes of excitation operators and truncating the series at the desired order, various levels of ADC theory are obtained. One aspect to note is that the excitation classes needed to construct a specific ADC level are directly connected to the order of perturbation theory. This can be easily seen in this illustration of the polarization propagator, where the zeroth and first order terms are related to single excitations (only one particle-hole pair is involved), while second order terms involve double excitations (two particle-hole pairs are involved). To illustrate this further, we list the explicit expressions for the ADC matrix \(\mathbf{M}\) in spin-orbitals up to second order [Wen16, Wor09]:
where \(\varepsilon_p\) are Hartree–Fock (HF) orbital energies, \(\braket{pq||rs}\) are anti-symmetrized two-electron integrals in physicists’ notation [SO12], \(\delta_{pq}\) is the Kronecker delta, and the \(t\)-amplitudes are \(t_{ijab} = \frac{\langle ab || ij \rangle}{\varepsilon_{a} + \varepsilon_{b} - \varepsilon_{i} - \varepsilon_{j}}\).
Explicit expressions for the effective transition amplitudes \(\mathbf{f}\) can be derived in an analogous manner. The necessary blocks through second order in perturbation theory are given as
where the operator \(\hat{P}_{pq}\) permutes the indices \(p\) and \(q\) in the following expression, and the second-order corrections to the ground-state density matrix \(\gamma_{ab}^{(2)}\) and \(\gamma_{ij}^{(2)}\) were defined here.
The structure of the ADC(2) matrix is depicted in panel (c) above. In principle, the ADC(2) matrix contains all the possible single and double excitations which can be constructed for the system of interest (using a particular basis set). However, to calculate all these excitations would be computationally very expensive or practically impossible for all but the smallest of systems. In practice, therefore, only the lowest \(n\) excited states are ever calculated by means of iterative diagonalization algorithms, where \(n\) is the number of states requested by the user. This means that the space of valence excitations is easily accessible, but makes the space of core excitations impossible to reach, except for molecules with very few electrons. An approach to overcome this problem will be discussed in more detail in the next section.
Excited-state properties#
A distinct advantage of the ISR over the classical propagator approach is that it gives direct access to excited-state wave functions by expanding it in the intermediate-state basis as
where the elements of the eigenvectors are the expansion coefficients, \(Y_{Jn} = \braket{\tilde{\Psi}_J | \Psi_n}\). This immediately offers the opportunity to calculate physical properties \(D_n\) of electronically excited state \(n\) via [ST04]
where \(\tilde{\mathbf{D}}\) is the representation of the operator \(\hat{D}\) corresponding to the observable in the intermediate state basis
The matrix \(\tilde{\mathbf{D}}\) has a perturbation expansion analogous to that of \(\mathbf{M}\) [ST04]. It should be noted that properties calculated in this manner generally differ from those calculated as derivatives of the energy \(E_n\) [HRDH19]. Transition moments between two different excited states (\(m \neq n\)) can be obtained in a completely analogous manner as
While explicit expressions for the ADC matrix \(\mathbf{M}\) are available through third order, the effective transition moments \(\mathbf{f}\) and property matrix \(\tilde{\mathbf{D}}\) are only available through second order. Combining the eigenvectors \(\mathbf{Y}\) (and eigenvalues) of the ADC(3) matrix together with the second-order descriptions of \(\mathbf{f}\) and \(\tilde{\mathbf{D}}\) yields transition moments, oscillator strengths and other properties at a level referred to as “ADC(3/2)” [ST04].
Size consistency#
As was discussed in previous sections, truncated CI schemes suffer from the size-consistency problem, while MP2 does not. For excited-state methods, we need to define size consistency somewhat differently. Imagine again two systems that are very far apart, such that they do not interact. For the ground-state energy, a size-consistent method has to give the same result for the composite system as the sum of the individual fragments. Concerning excitation energies, the result for one of the fragments should be the same when we apply the method to the individual fragment or to the composite system and look at the local excitations on the respective fragment (to be more specific, this is referred to as size intensivity). We will check this in the following for a system consisting of two small molecules for ADC(1) and ADC(2).
import veloxchem as vlx
import gator
from gator.adconedriver import AdcOneDriver
from gator.adctwodriver import AdcTwoDriver
import numpy as np
np.set_printoptions(precision=5, suppress=True)
# LiH molecule
lih_xyz="""2
Li 0.000000 0.000000 0.000000
H 0.000000 0.000000 1.000000
"""
lih = vlx.Molecule.read_xyz_string(lih_xyz)
# Water molecule
h2o_xyz = """3
O 0.000000000000 0.000000000000 0.000000000000
H 0.000000000000 0.740848095288 0.582094932012
H 0.000000000000 -0.740848095288 0.582094932012
"""
h2o = vlx.Molecule.read_xyz_string(h2o_xyz)
# Basis set
basis_set_label = "6-31g"
basis_lih = vlx.MolecularBasis.read(lih, basis_set_label)
basis_h2o = vlx.MolecularBasis.read(h2o, basis_set_label)
3Dmol.js failed to load for some reason. Please check your browser console for error messages.
Calculate HF reference states#
# SCF will be run by VeloxChem through Gator
scf_lih = gator.run_scf(lih, basis_lih, conv_thresh=1e-10, verbose=False)
scf_h2o = gator.run_scf(h2o, basis_h2o, conv_thresh=1e-10, verbose=False)
e_scf_lih = scf_lih.get_scf_energy()
e_scf_h2o = scf_h2o.get_scf_energy()
Excitation energies of individual systems#
# Number of excited states for H2O, twice as many for LiH, thrice for composite system
nexc = 3
# Calculate ADC(1) and ADC(2) excitation energies with Gator
adc1_drv = AdcOneDriver(scf_lih.comm)
adc1_drv.conv_thresh = 1e-5
adc1_results_h2o = adc1_drv.compute(h2o, basis_h2o, scf_h2o.scf_tensors)
adc1_drv.nstates = 2 * nexc
adc1_results_lih = adc1_drv.compute(lih, basis_lih, scf_lih.scf_tensors)
adc2_drv = AdcTwoDriver(scf_lih.comm, scf_lih.ostream)
adc2_drv.conv_thresh = 1e-5
adc2_results_h2o = adc2_drv.compute(h2o, basis_h2o, scf_h2o.scf_tensors)
adc2_drv.nstates = 2 * nexc
adc2_results_lih = adc2_drv.compute(lih, basis_lih, scf_lih.scf_tensors)
Show code cell output
ADC(1) Driver Setup
=====================
Number Of Excited States : 3
Max. Number Of Iterations : 50
Convergence Threshold : 1.0e-05
ERI Screening Threshold : 1.0e-15
* Info * Number of occupied orbitals: 5
* Info * Number of virtual orbitals: 8
MO Integrals Driver Setup
===========================
ERI Screening Threshold : 1.0e-15
Batch Size of Fock Matrices : 100
* Info * Processing Fock builds for the OO block...
* Info * batch 1/1
* Info * Integrals transformation for the OO block done in 0.21 sec. Load imb.: 0.0 %
*** Iteration: 1 * Reduced Space: 3 * Residues (Max,Min): 1.49e-01 and 1.15e-01
State 1: 0.36669368 au Residual Norm: 0.11478601
State 2: 0.44840498 au Residual Norm: 0.13775605
State 3: 0.46360595 au Residual Norm: 0.14905941
*** Iteration: 2 * Reduced Space: 6 * Residues (Max,Min): 4.52e-02 and 1.08e-03
State 1: 0.35291511 au Residual Norm: 0.01136344
State 2: 0.42544431 au Residual Norm: 0.00107731
State 3: 0.44554970 au Residual Norm: 0.04521708
*** Iteration: 3 * Reduced Space: 9 * Residues (Max,Min): 7.67e-03 and 1.36e-05
State 1: 0.35279762 au Residual Norm: 0.00151889
State 2: 0.42544293 au Residual Norm: 0.00001364
State 3: 0.44369379 au Residual Norm: 0.00767191
*** Iteration: 4 * Reduced Space: 12 * Residues (Max,Min): 2.29e-03 and 6.48e-16
State 1: 0.35279702 au Residual Norm: 0.00033748
State 2: 0.42544293 au Residual Norm: 0.00000000
State 3: 0.44360836 au Residual Norm: 0.00228847
*** Iteration: 5 * Reduced Space: 15 * Residues (Max,Min): 9.04e-04 and 3.41e-15
State 1: 0.35279701 au Residual Norm: 0.00000637
State 2: 0.42544293 au Residual Norm: 0.00000000
State 3: 0.44360608 au Residual Norm: 0.00090417
*** Iteration: 6 * Reduced Space: 18 * Residues (Max,Min): 1.10e-04 and 5.69e-15
State 1: 0.35279701 au Residual Norm: 0.00000010
State 2: 0.42544293 au Residual Norm: 0.00000000
State 3: 0.44360599 au Residual Norm: 0.00010954
*** Iteration: 7 * Reduced Space: 21 * Residues (Max,Min): 4.73e-06 and 4.85e-15
State 1: 0.35279701 au Residual Norm: 0.00000001
State 2: 0.42544293 au Residual Norm: 0.00000000
State 3: 0.44360599 au Residual Norm: 0.00000473
*** 3 excited states converged in 7 iterations. Time: 0.23 sec.
ADC(1) excited states
---------------------
Excited State S1: 0.35279701 a.u. 9.60010 eV Osc.Str. 0.01663
Excited State S2: 0.42544293 a.u. 11.57689 eV Osc.Str. 0.00000
Excited State S3: 0.44360599 a.u. 12.07113 eV Osc.Str. 0.11240
ADC(1) Driver Setup
=====================
Number Of Excited States : 6
Max. Number Of Iterations : 50
Convergence Threshold : 1.0e-05
ERI Screening Threshold : 1.0e-15
* Info * Number of occupied orbitals: 2
* Info * Number of virtual orbitals: 9
MO Integrals Driver Setup
===========================
ERI Screening Threshold : 1.0e-15
Batch Size of Fock Matrices : 100
* Info * Processing Fock builds for the OO block...
* Info * batch 1/1
* Info * Integrals transformation for the OO block done in 0.04 sec. Load imb.: 0.0 %
*** Iteration: 1 * Reduced Space: 6 * Residues (Max,Min): 3.60e-02 and 1.47e-02
State 1: 0.15889294 au Residual Norm: 0.01952183
State 2: 0.20608326 au Residual Norm: 0.01468372
State 3: 0.21659287 au Residual Norm: 0.03602681
State 4: 0.28273182 au Residual Norm: 0.01773908
State 5: 0.33269430 au Residual Norm: 0.01820955
State 6: 0.33539479 au Residual Norm: 0.02560730
*** Iteration: 2 * Reduced Space: 12 * Residues (Max,Min): 4.60e-02 and 2.00e-15
State 1: 0.15870155 au Residual Norm: 0.00048111
State 2: 0.20597994 au Residual Norm: 0.00000000
State 3: 0.20599656 au Residual Norm: 0.00587184
State 4: 0.28256950 au Residual Norm: 0.00084005
State 5: 0.33252586 au Residual Norm: 0.00000000
State 6: 0.33360191 au Residual Norm: 0.04595089
*** Iteration: 3 * Reduced Space: 17 * Residues (Max,Min): 4.17e-05 and 1.63e-10
State 1: 0.15870142 au Residual Norm: 0.00001296
State 2: 0.20597994 au Residual Norm: 0.00000000
State 3: 0.20597994 au Residual Norm: 0.00000011
State 4: 0.28256876 au Residual Norm: 0.00004166
State 5: 0.33252586 au Residual Norm: 0.00000000
State 6: 0.33252586 au Residual Norm: 0.00000533
*** Iteration: 4 * Reduced Space: 18 * Residues (Max,Min): 8.21e-15 and 8.85e-17
State 1: 0.15870142 au Residual Norm: 0.00000000
State 2: 0.20597994 au Residual Norm: 0.00000000
State 3: 0.20597994 au Residual Norm: 0.00000000
State 4: 0.28256876 au Residual Norm: 0.00000000
State 5: 0.33252586 au Residual Norm: 0.00000000
State 6: 0.33252586 au Residual Norm: 0.00000000
*** 6 excited states converged in 4 iterations. Time: 0.06 sec.
ADC(1) excited states
---------------------
Excited State S1: 0.15870142 a.u. 4.31849 eV Osc.Str. 0.02843
Excited State S2: 0.20597994 a.u. 5.60500 eV Osc.Str. 0.25169
Excited State S3: 0.20597994 a.u. 5.60500 eV Osc.Str. 0.25169
Excited State S4: 0.28256876 a.u. 7.68909 eV Osc.Str. 0.04341
Excited State S5: 0.33252586 a.u. 9.04849 eV Osc.Str. 0.02652
Excited State S6: 0.33252586 a.u. 9.04849 eV Osc.Str. 0.02652
MO Integrals Driver Setup
===========================
ERI Screening Threshold : 1.0e-15
Batch Size of Fock Matrices : 100
* Info * Processing Fock builds for the OO block...
* Info * batch 1/1
* Info * Integrals transformation for the OO block done in 0.11 sec. Load imb.: 0.0 %
* Info * Processing Fock builds for the VV block...
* Info * batch 1/1
* Info * Integrals transformation for the VV block done in 0.05 sec. Load imb.: 0.0 %
* Info * Processing Fock builds for the OV block...
* Info * batch 1/1
* Info * Integrals transformation for the OV block done in 0.10 sec. Load imb.: 0.0 %
* Info * 146.62 kB of memory used for MO integrals on the master node.
* Info * 6.19 GB of memory available on the master node.
* Info * Time spent in calculating memory usage: 0.00 sec.
ADC(2) Driver Setup
=====================
Number Of Excited States : 3
Max. Number Of Iterations : 150
Convergence Threshold : 1.0e-05
ERI Screening Threshold : 1.0e-15
ADC(1) Driver Setup
=====================
Number Of Excited States : 3
Max. Number Of Iterations : 50
Convergence Threshold : 1.0e-04
ERI Screening Threshold : 1.0e-15
* Info * Number of occupied orbitals: 5
* Info * Number of virtual orbitals: 8
*** Iteration: 1 * Reduced Space: 3 * Residues (Max,Min): 1.49e-01 and 1.15e-01
State 1: 0.36669368 au Residual Norm: 0.11478601
State 2: 0.44840498 au Residual Norm: 0.13775605
State 3: 0.46360595 au Residual Norm: 0.14905941
*** Iteration: 2 * Reduced Space: 6 * Residues (Max,Min): 4.52e-02 and 1.08e-03
State 1: 0.35291511 au Residual Norm: 0.01136344
State 2: 0.42544431 au Residual Norm: 0.00107731
State 3: 0.44554970 au Residual Norm: 0.04521708
*** Iteration: 3 * Reduced Space: 9 * Residues (Max,Min): 7.67e-03 and 1.36e-05
State 1: 0.35279762 au Residual Norm: 0.00151889
State 2: 0.42544293 au Residual Norm: 0.00001364
State 3: 0.44369379 au Residual Norm: 0.00767191
*** Iteration: 4 * Reduced Space: 12 * Residues (Max,Min): 2.29e-03 and 3.90e-16
State 1: 0.35279702 au Residual Norm: 0.00033748
State 2: 0.42544293 au Residual Norm: 0.00000000
State 3: 0.44360836 au Residual Norm: 0.00228847
*** Iteration: 5 * Reduced Space: 15 * Residues (Max,Min): 9.02e-04 and 2.14e-15
State 1: 0.35279701 au Residual Norm: 0.00000509
State 2: 0.42544293 au Residual Norm: 0.00000000
State 3: 0.44360608 au Residual Norm: 0.00090170
*** Iteration: 6 * Reduced Space: 18 * Residues (Max,Min): 1.10e-04 and 4.41e-15
State 1: 0.35279701 au Residual Norm: 0.00000013
State 2: 0.42544293 au Residual Norm: 0.00000000
State 3: 0.44360599 au Residual Norm: 0.00010957
*** Iteration: 7 * Reduced Space: 21 * Residues (Max,Min): 6.37e-06 and 9.93e-15
State 1: 0.35279701 au Residual Norm: 0.00000002
State 2: 0.42544293 au Residual Norm: 0.00000000
State 3: 0.44360599 au Residual Norm: 0.00000637
*** 3 excited states converged in 7 iterations. Time: 0.01 sec.
ADC(1) excited states
---------------------
Excited State S1: 0.35279701 a.u. 9.60010 eV Osc.Str. 0.01663
Excited State S2: 0.42544293 a.u. 11.57689 eV Osc.Str. 0.00000
Excited State S3: 0.44360599 a.u. 12.07113 eV Osc.Str. 0.11240
* Info * Number of occupied orbitals: 5
* Info * Number of virtual orbitals: 8
* Info * MP2 correlation energy: -0.1274706653 a.u. Time: 0.00 sec.
* Info * Initial guess generated in 0.01 sec.
*** Iteration: 1 * Reduced Space: 3 * Residual Norm: 6.71e-02
State 1: 0.35279701 au Eigenvalue Error: 3.98e-02
*** Iteration: 2 * Reduced Space: 6 * Residual Norm: 5.50e-03
State 1: 0.31462536 au Eigenvalue Error: 2.87e-03
* Info * Collapsing subspace...
*** Iteration: 3 * Reduced Space: 6 * Residual Norm: 3.42e-04
State 1: 0.31187300 au Eigenvalue Error: 1.74e-05
* Info * Collapsing subspace...
*** Iteration: 4 * Reduced Space: 6 * Residual Norm: 6.09e-05
State 1: 0.31185626 au Eigenvalue Error: 1.01e-07
*** Iteration: 5 * Reduced Space: 9 * Residual Norm: 1.21e-05
State 1: 0.31185616 au Eigenvalue Error: 9.50e-10
*** Iteration: 6 * Reduced Space: 12 * Residual Norm: 3.49e-07
State 1: 0.31185616 au converged
* Info * State 1 is converged.
*** Iteration: 7 * Reduced Space: 15 * Residual Norm: 3.61e-03
State 1: 0.31185616 au converged
State 2: 0.40125793 au Eigenvalue Error: 3.21e-03
* Info * Collapsing subspace...
*** Iteration: 8 * Reduced Space: 6 * Residual Norm: 5.23e-05
State 1: 0.31185616 au converged
State 2: 0.39816818 au Eigenvalue Error: 3.08e-06
*** Iteration: 9 * Reduced Space: 9 * Residual Norm: 9.73e-07
State 1: 0.31185616 au converged
State 2: 0.39816521 au Eigenvalue Error: 3.57e-09
*** Iteration: 10 * Reduced Space: 12 * Residual Norm: 5.74e-08
State 1: 0.31185616 au converged
State 2: 0.39816520 au converged
* Info * State 2 is converged.
*** Iteration: 11 * Reduced Space: 14 * Residual Norm: 2.40e-04
State 1: 0.31185616 au converged
State 2: 0.39816520 au converged
State 3: 0.40309707 au Eigenvalue Error: 2.19e-04
* Info * Collapsing subspace...
*** Iteration: 12 * Reduced Space: 6 * Residual Norm: 1.01e-05
State 1: 0.31185616 au converged
State 2: 0.39816520 au converged
State 3: 0.40288697 au Eigenvalue Error: 1.01e-08
*** Iteration: 13 * Reduced Space: 9 * Residual Norm: 2.89e-06
State 1: 0.31185616 au converged
State 2: 0.39816520 au converged
State 3: 0.40288696 au converged
* Info * State 3 is converged.
* Info * Total number of sigma builds: 63
* Info * Average time per sigma build: 0.00 sec
* Info * Total number of d_sigma builds: 13
* Info * Average time per d_sigma build: 0.00 sec
*** 3 excited states converged in 13 iterations. Time: 0.49 sec.
ADC(2) excited states
---------------------
Excited State S1: 0.31185616 a.u. 8.48604 eV |v1|^2=0.9595
Excited State S2: 0.39816520 a.u. 10.83463 eV |v1|^2=0.9638
Excited State S3: 0.40288696 a.u. 10.96311 eV |v1|^2=0.9573
State S1
-------------------------------
HOMO -> LUMO 0.9772
HOMO -> LUMO+4 -0.0541
State S2
-------------------------------
HOMO -> LUMO+1 0.9765
HOMO -> LUMO+6 0.0824
HOMO -> LUMO+2 -0.0588
State S3
-------------------------------
HOMO-1 -> LUMO -0.9722
HOMO-2 -> LUMO+1 0.0749
MO Integrals Driver Setup
===========================
ERI Screening Threshold : 1.0e-15
Batch Size of Fock Matrices : 100
* Info * Processing Fock builds for the OO block...
* Info * batch 1/1
* Info * Integrals transformation for the OO block done in 0.01 sec. Load imb.: 0.0 %
* Info * Processing Fock builds for the VV block...
* Info * batch 1/1
* Info * Integrals transformation for the VV block done in 0.05 sec. Load imb.: 0.0 %
* Info * Processing Fock builds for the OV block...
* Info * batch 1/1
* Info * Integrals transformation for the OV block done in 0.03 sec. Load imb.: 0.0 %
* Info * 71.79 kB of memory used for MO integrals on the master node.
* Info * 6.19 GB of memory available on the master node.
* Info * Time spent in calculating memory usage: 0.00 sec.
ADC(2) Driver Setup
=====================
Number Of Excited States : 6
Max. Number Of Iterations : 150
Convergence Threshold : 1.0e-05
ERI Screening Threshold : 1.0e-15
ADC(1) Driver Setup
=====================
Number Of Excited States : 6
Max. Number Of Iterations : 50
Convergence Threshold : 1.0e-04
ERI Screening Threshold : 1.0e-15
* Info * Number of occupied orbitals: 2
* Info * Number of virtual orbitals: 9
*** Iteration: 1 * Reduced Space: 6 * Residues (Max,Min): 3.60e-02 and 1.47e-02
State 1: 0.15889294 au Residual Norm: 0.01952183
State 2: 0.20608326 au Residual Norm: 0.01468372
State 3: 0.21659287 au Residual Norm: 0.03602681
State 4: 0.28273182 au Residual Norm: 0.01773908
State 5: 0.33269430 au Residual Norm: 0.01820955
State 6: 0.33539479 au Residual Norm: 0.02560730
*** Iteration: 2 * Reduced Space: 12 * Residues (Max,Min): 4.60e-02 and 1.12e-14
State 1: 0.15870155 au Residual Norm: 0.00048111
State 2: 0.20597994 au Residual Norm: 0.00000000
State 3: 0.20599656 au Residual Norm: 0.00587184
State 4: 0.28256950 au Residual Norm: 0.00084005
State 5: 0.33252586 au Residual Norm: 0.00000000
State 6: 0.33360191 au Residual Norm: 0.04595089
*** Iteration: 3 * Reduced Space: 16 * Residues (Max,Min): 6.88e-05 and 6.00e-13
State 1: 0.15870142 au Residual Norm: 0.00001296
State 2: 0.20597994 au Residual Norm: 0.00000000
State 3: 0.20597994 au Residual Norm: 0.00000473
State 4: 0.28256876 au Residual Norm: 0.00004260
State 5: 0.33252586 au Residual Norm: 0.00000000
State 6: 0.33252586 au Residual Norm: 0.00006878
*** 6 excited states converged in 3 iterations. Time: 0.00 sec.
ADC(1) excited states
---------------------
Excited State S1: 0.15870142 a.u. 4.31849 eV Osc.Str. 0.02843
Excited State S2: 0.20597994 a.u. 5.60500 eV Osc.Str. 0.25169
Excited State S3: 0.20597994 a.u. 5.60500 eV Osc.Str. 0.25169
Excited State S4: 0.28256876 a.u. 7.68909 eV Osc.Str. 0.04341
Excited State S5: 0.33252586 a.u. 9.04849 eV Osc.Str. 0.02652
Excited State S6: 0.33252586 a.u. 9.04849 eV Osc.Str. 0.02652
* Info * Number of occupied orbitals: 2
* Info * Number of virtual orbitals: 9
* Info * MP2 correlation energy: -0.0136828971 a.u. Time: 0.00 sec.
* Info * Initial guess generated in 0.01 sec.
*** Iteration: 1 * Reduced Space: 6 * Residual Norm: 1.82e-02
State 1: 0.15870142 au Eigenvalue Error: 1.76e-02
*** Iteration: 2 * Reduced Space: 12 * Residual Norm: 1.26e-03
State 1: 0.14174508 au Eigenvalue Error: 6.10e-05
* Info * Collapsing subspace...
*** Iteration: 3 * Reduced Space: 12 * Residual Norm: 6.25e-05
State 1: 0.14168622 au Eigenvalue Error: 1.61e-06
*** Iteration: 4 * Reduced Space: 16 * Residual Norm: 1.55e-06
State 1: 0.14168468 au Eigenvalue Error: 2.05e-09
*** Iteration: 5 * Reduced Space: 18 * Residual Norm: 1.22e-08
State 1: 0.14168467 au converged
* Info * State 1 is converged.
*** Iteration: 6 * Reduced Space: 18 * Residual Norm: 1.68e-03
State 1: 0.14168467 au converged
State 2: 0.18797246 au Eigenvalue Error: 1.66e-03
* Info * Collapsing subspace...
*** Iteration: 7 * Reduced Space: 12 * Residual Norm: 3.55e-07
State 1: 0.14168467 au converged
State 2: 0.18637063 au Eigenvalue Error: 3.55e-07
*** Iteration: 8 * Reduced Space: 17 * Residual Norm: 1.66e-09
State 1: 0.14168467 au converged
State 2: 0.18637029 au converged
* Info * State 2 is converged.
*** Iteration: 9 * Reduced Space: 18 * Residual Norm: 1.36e-08
State 1: 0.14168467 au converged
State 2: 0.18637029 au converged
State 3: 0.18637028 au Eigenvalue Error: 1.35e-08
* Info * Collapsing subspace...
*** Iteration: 10 * Reduced Space: 12 * Residual Norm: 6.19e-10
State 1: 0.14168467 au converged
State 2: 0.18637029 au converged
State 3: 0.18637029 au converged
* Info * State 3 is converged.
*** Iteration: 11 * Reduced Space: 17 * Residual Norm: 2.81e-03
State 1: 0.14168467 au converged
State 2: 0.18637029 au converged
State 3: 0.18637029 au converged
State 4: 0.26955011 au Eigenvalue Error: 2.69e-03
* Info * Collapsing subspace...
*** Iteration: 12 * Reduced Space: 12 * Residual Norm: 3.82e-05
State 1: 0.14168467 au converged
State 2: 0.18637029 au converged
State 3: 0.18637029 au converged
State 4: 0.26694944 au Eigenvalue Error: 1.60e-06
*** Iteration: 13 * Reduced Space: 17 * Residual Norm: 1.26e-07
State 1: 0.14168467 au converged
State 2: 0.18637029 au converged
State 3: 0.18637029 au converged
State 4: 0.26694790 au converged
* Info * State 4 is converged.
*** Iteration: 14 * Reduced Space: 18 * Residual Norm: 1.85e-03
State 1: 0.14168467 au converged
State 2: 0.18637029 au converged
State 3: 0.18637029 au converged
State 4: 0.26694790 au converged
State 5: 0.32063129 au Eigenvalue Error: 1.75e-03
* Info * Collapsing subspace...
*** Iteration: 15 * Reduced Space: 12 * Residual Norm: 3.53e-05
State 1: 0.14168467 au converged
State 2: 0.18637029 au converged
State 3: 0.18637029 au converged
State 4: 0.26694790 au converged
State 5: 0.31893708 au Eigenvalue Error: 1.71e-06
*** Iteration: 16 * Reduced Space: 17 * Residual Norm: 2.07e-08
State 1: 0.14168467 au converged
State 2: 0.18637029 au converged
State 3: 0.18637029 au converged
State 4: 0.26694790 au converged
State 5: 0.31893873 au converged
* Info * State 5 is converged.
*** Iteration: 17 * Reduced Space: 18 * Residual Norm: 3.06e-05
State 1: 0.14168467 au converged
State 2: 0.18637029 au converged
State 3: 0.18637029 au converged
State 4: 0.26694790 au converged
State 5: 0.31893873 au converged
State 6: 0.31996133 au Eigenvalue Error: 2.96e-05
* Info * Collapsing subspace...
*** Iteration: 18 * Reduced Space: 12 * Residual Norm: 3.43e-10
State 1: 0.14168467 au converged
State 2: 0.18637029 au converged
State 3: 0.18637029 au converged
State 4: 0.26694790 au converged
State 5: 0.31893873 au converged
State 6: 0.31993255 au converged
* Info * State 6 is converged.
* Info * Total number of sigma builds: 131
* Info * Average time per sigma build: 0.00 sec
* Info * Total number of d_sigma builds: 18
* Info * Average time per d_sigma build: 0.00 sec
*** 6 excited states converged in 18 iterations. Time: 0.37 sec.
ADC(2) excited states
---------------------
Excited State S1: 0.14168467 a.u. 3.85544 eV |v1|^2=0.9645
Excited State S2: 0.18637029 a.u. 5.07139 eV |v1|^2=0.9634
Excited State S3: 0.18637029 a.u. 5.07139 eV |v1|^2=0.9634
Excited State S4: 0.26694790 a.u. 7.26402 eV |v1|^2=0.9652
Excited State S5: 0.31893873 a.u. 8.67876 eV |v1|^2=0.9662
Excited State S6: 0.31993255 a.u. 8.70581 eV |v1|^2=0.9719
State S1
-------------------------------
HOMO -> LUMO 0.9487
HOMO -> LUMO+4 -0.2366
HOMO -> LUMO+3 -0.0915
State S2
-------------------------------
HOMO -> LUMO+2 0.9426
HOMO -> LUMO+5 0.2700
State S3
-------------------------------
HOMO -> LUMO+1 0.9426
HOMO -> LUMO+6 0.2700
State S4
-------------------------------
HOMO -> LUMO+3 -0.9756
HOMO -> LUMO+4 0.0876
HOMO -> LUMO -0.0741
State S5
-------------------------------
HOMO -> LUMO+4 -0.9512
HOMO -> LUMO -0.2365
HOMO -> LUMO+3 -0.0707
State S6
-------------------------------
HOMO -> LUMO+5 -0.9453
HOMO -> LUMO+2 0.2670
HOMO -> LUMO+6 0.0825
print("LiH ADC(1) excitation energies:\n", adc1_results_lih['eigenvalues'])
print("\nH2O ADC(1) excitation energies:\n", adc1_results_h2o['eigenvalues'])
print("\nLiH ADC(2) excitation energies:\n", adc2_results_lih['eigenvalues'])
print("\nH2O ADC(2) excitation energies:\n", adc2_results_h2o['eigenvalues'])
LiH ADC(1) excitation energies:
[0.1587 0.20598 0.20598 0.28257 0.33253 0.33253]
H2O ADC(1) excitation energies:
[0.3528 0.42544 0.44361]
LiH ADC(2) excitation energies:
[0.14168 0.18637 0.18637 0.26695 0.31894 0.31993]
H2O ADC(2) excitation energies:
[0.31186 0.39817 0.40289]
Composite system#
# LiH and H2O molecules 100 Å apart
lih_h2o_xyz="""5
Li 0.000000 0.000000 0.000000
H 0.000000 0.000000 1.000000
O 100.000000000000 0.000000000000 0.000000000000
H 100.000000000000 0.740848095288 0.582094932012
H 100.000000000000 -0.740848095288 0.582094932012
"""
lih_h2o = vlx.Molecule.read_xyz_string(lih_h2o_xyz)
basis_lih_h2o = vlx.MolecularBasis.read(lih_h2o, basis_set_label)
# Run SCF of composite system and compare to sum of individual SCF energies
scf_lih_h2o = gator.run_scf(lih_h2o, basis_lih_h2o, conv_thresh=1e-10, verbose=False)
print("Sum of SCF: ", e_scf_lih + e_scf_h2o, "au")
Show code cell source
print("Sum of SCF: ", e_scf_lih + e_scf_h2o, "au")
Sum of SCF: -83.85469422644589 au
adc1_drv.nstates = 3 * nexc
adc1_results_lih_h2o = adc1_drv.compute(lih_h2o, basis_lih_h2o, scf_lih_h2o.scf_tensors)
adc2_drv.nstates = 3 * nexc
adc2_results_lih_h2o = adc2_drv.compute(lih_h2o, basis_lih_h2o, scf_lih_h2o.scf_tensors)
Show code cell source
print("LiH ADC(1) excitation energies:\n", adc1_results_lih['eigenvalues'])
print("\nH2O ADC(1) excitation energies:\n", adc1_results_h2o['eigenvalues'])
print("\nLiH and H2O ADC(1) excitation energies:\n", adc1_results_lih_h2o['eigenvalues'])
print("\nLiH ADC(2) excitation energies:\n", adc2_results_lih['eigenvalues'])
print("\nH2O ADC(2) excitation energies:\n", adc2_results_h2o['eigenvalues'])
print("\nLiH and H2O ADC(2) excitation energies:\n", adc2_results_lih_h2o['eigenvalues'])
LiH ADC(1) excitation energies:
[0.1587 0.20598 0.20598 0.28257 0.33253 0.33253]
H2O ADC(1) excitation energies:
[0.3528 0.42544 0.44361]
LiH and H2O ADC(1) excitation energies:
[0.1587 0.20598 0.20598 0.28257 0.33253 0.33253 0.33477 0.3528 0.44361]
LiH ADC(2) excitation energies:
[0.14168 0.18637 0.18637 0.26695 0.31894 0.31993]
H2O ADC(2) excitation energies:
[0.31186 0.39817 0.40289]
LiH and H2O ADC(2) excitation energies:
[0.14169 0.18637 0.18637 0.26695 0.31186 0.31894 0.31993 0.31993 0.39817]
As we can see, the excitation energies of the individual LiH molecule occur also in the composite system, both at the ADC(1) and ADC(2) levels. At higher excitation energies, also the ones from water occur again. This means that the ADC(\(n\)) approaches are indeed size consistent (or size intensive). The interested reader can confirm the same finding also for the transition moments or oscillator strengths.
Note
Since ADC(1) is in fact equivalent to configuration interaction singles (CIS) for excitation energies and excited-state properties, this means that CIS is the only truncated CI approach that is size consistent.