Non-standard calculations#
In this chapter we will consider some non-standard calculations. Some can be useful but need care for practical considerations (i.e. transient X-ray spectroscopy), and some are more illustrations of alternative (but not recommended) ways of modelling spectra. Be careful before directly adopting these approaches for some practical problem.
Loading modules and routines:
import copy
import adcc
import matplotlib.pyplot as plt
import numpy as np
import veloxchem as vlx
def lorentzian(x, y, xmin, xmax, xstep, gamma):
xi = np.arange(xmin, xmax, xstep)
yi = np.zeros(len(xi))
for i in range(len(xi)):
for k in range(len(x)):
yi[i] = yi[i] + y[k] * (gamma / 2.0) / (
(xi[i] - x[k]) ** 2 + (gamma / 2.0) ** 2
)
return xi, yi
au2ev = 27.211386
Transient X-ray absorption spectroscopy#
An increasingly large field of study is to use a pump-probe protocol, where some chemical reaction is initiated by some pump (typically a laser), and the dynamics are then probed using some X-ray spectroscopy. The modeling of such process is quite new, and we will here present some protocols of how such processes can be considered.
Valence-excited reference state#
By using an excited state as the references state, the X-ray absorption spectra can be considered in a manner similar to XES:
Perform a ground state calculation
Use the result as initial guess for a second calculation, where the occupations are changed to emulate that of the desired (valence) excited state
Perform a wave function optimization with above configuration, using a constraint such as MOM to avoid a collapse to the ground state
Calculate the X-ray absorption spectra of this reference state
When considering (singlet) valence-excitations of a closed-shell molecule, two different reference state spin-muliticiplicity configurations are possible:
Low-spin open-shell reference (LSOR), which moves an electron within the same multiplicity
High-spin open-shell reference (HSOR), which flips the spin of the moved electron, and thus forms a triplet reference state (when considering singlet excitations of a closed-shell system)
Note that the LSOR wave function will be heavily spin contaminated, as seen below. This has been claimed to lead to minimal errors, but care should be taken. Further note that converging to a reference state which represents the actual valence excitation is non-trivial, and may indeed be all but impossible. As such, this two-step approach is useful, but has some issues. Finally, if using correlated methods, there are some concerns that the observed relative energies are off from experimental values, which could relate to issues with using a non-Aufbau reference state.
As an example we consider the first valence-excited state of water:
Note
pyscf version - to be changed
water_xyz = """
O 0.0000000000 0.0000000000 0.1178336003
H -0.7595754146 -0.0000000000 -0.4713344012
H 0.7595754146 0.0000000000 -0.4713344012
"""
mol = gto.Mole()
mol.atom = water_xyz
mol.basis = "6-31G"
mol.build()
print('GS:')
scf_gs = scf.UHF(mol)
scf_gs.kernel()
print('LSOR:')
mo0 = copy.deepcopy(scf_gs.mo_coeff)
occ0 = copy.deepcopy(scf_gs.mo_occ)
occ0[0][4] = 0.0
occ0[0][5] = 1.0
scf_lsor = scf.UHF(mol)
scf.addons.mom_occ(scf_lsor, mo0, occ0)
scf_lsor.kernel()
print('HSOR:')
mo0 = copy.deepcopy(scf_gs.mo_coeff)
occ0 = copy.deepcopy(scf_gs.mo_occ)
occ0[0][4] = 0.0
occ0[1][5] = 1.0
scf_hsor = scf.UHF(mol)
scf.addons.mom_occ(scf_hsor, mo0, occ0)
scf_hsor.kernel()
As can be seen, the \(\langle S^2 \rangle\) of the LSOR reference is close to 1, and thus represents an almost perfect mix of a singlet and triplet.
Calculating the valence-excitation energies and comparing it to energy differences obtained from the different reference states:
adc_gs = adcc.adc2(scf_gs, n_states=5)
adc_xas = adcc.cvs_adc2(scf_gs, n_states=5, core_orbitals=1)
adc_lsor = adcc.cvs_adc2(scf_lsor, n_states=5, core_orbitals=1)
adc_hsor = adcc.cvs_adc2(scf_hsor, n_states=5, core_orbitals=1)
print(adc_gs.describe())
print(27.2114 * (adc_gs.ground_state.energy() - adc_lsor.ground_state.energy()))
print(27.2114 * (adc_gs.ground_state.energy() - adc_hsor.ground_state.energy()))
The first allowed transition energy is relatively close to the \(\Delta\)MP2 results (as we use the MP2 energies), in particular for the LSOR. Resulting spectra can now be plotted as:
plt.figure(figsize=(6,3))
adc_xas.plot_spectrum(label="GS")
adc_lsor.plot_spectrum(label="LSOR")
adc_hsor.plot_spectrum(label="HSOR")
plt.legend()
plt.show()
We see the occurance of a lower-energy feature, representing the 1s to SOMO transition, as well as an upward shift of remaining features.
Coupling valence- and core-excited eigenstates#
To be added
Impact of channel restriction for TDDFT#
The influence of channel-restriction/CVS schemes for TDDFT can be considered for smaller systems by diagonalizing the full-space and CVS-space matrices, thus constructing the total global spectrum. This will not be possible for larger systems/basis sets, or for correlated method, where other CVS relaxation schemes have been used instead.
water_mol_str = """
O 0.0000000000 0.0000000000 0.1178336003
H -0.7595754146 -0.0000000000 -0.4713344012
H 0.7595754146 0.0000000000 -0.4713344012
"""
basis = "6-31G"
vlx_mol = vlx.Molecule.read_molecule_string(water_mol_str)
vlx_bas = vlx.MolecularBasis.read(vlx_mol, basis)
scf_drv = vlx.ScfRestrictedDriver()
scf_settings = {"conv_thresh": 1.0e-6}
method_settings = {"xcfun": "b3lyp"}
scf_drv.update_settings(scf_settings, method_settings)
scf_results = scf_drv.compute(vlx_mol, vlx_bas)
Show code cell output
* Info * Reading basis set from file: /home/emi/miniconda3/envs/echem/lib/python3.11/site-packages/veloxchem/basis/6-31G
Molecular Basis (Atomic Basis)
================================
Basis: 6-31G
Atom Contracted GTOs Primitive GTOs
O (3S,2P) (10S,4P)
H (2S) (4S)
Contracted Basis Functions : 13
Primitive Basis Functions : 30
Self Consistent Field Driver Setup
====================================
Wave Function Model : Spin-Restricted Kohn-Sham
Initial Guess Model : Superposition of Atomic Densities
Convergence Accelerator : Two Level Direct Inversion of Iterative Subspace
Max. Number of Iterations : 50
Max. Number of Error Vectors : 10
Convergence Threshold : 1.0e-06
ERI Screening Scheme : Cauchy Schwarz + Density
ERI Screening Mode : Dynamic
ERI Screening Threshold : 1.0e-12
Linear Dependence Threshold : 1.0e-06
Exchange-Correlation Functional : B3LYP
Molecular Grid Level : 4
* Info * Nuclear repulsion energy: 9.1561447194 a.u.
* Info * Using the Libxc library (version 6.2.2).
S. Lehtola, C. Steigemann, M. J.T. Oliveira, and M. A.L. Marques., SoftwareX 7, 1–5 (2018)
* Info * Using the B3LYP functional.
P. J. Stephens, F. J. Devlin, C. F. Chabalowski, and M. J. Frisch., J. Phys. Chem. 98, 11623 (1994)
* Info * Molecular grid with 40792 points generated in 0.02 sec.
* Info * Overlap matrix computed in 0.00 sec.
* Info * Kinetic energy matrix computed in 0.00 sec.
* Info * Nuclear potential matrix computed in 0.00 sec.
* Info * Orthogonalization matrix computed in 0.00 sec.
* Info * SAD initial guess computed in 0.00 sec.
* Info * Starting Reduced Basis SCF calculation...
* Info * ...done. SCF energy in reduced basis set: -75.983870205310 a.u. Time: 0.03 sec.
* Info * Overlap matrix computed in 0.00 sec.
* Info * Kinetic energy matrix computed in 0.00 sec.
* Info * Nuclear potential matrix computed in 0.00 sec.
* Info * Orthogonalization matrix computed in 0.00 sec.
Iter. | Kohn-Sham Energy | Energy Change | Gradient Norm | Max. Gradient | Density Change
--------------------------------------------------------------------------------------------
1 -76.384872592259 0.0000000000 0.05814060 0.01079184 0.00000000
2 -76.384686594376 0.0001859979 0.07420221 0.01375784 0.03127402
3 -76.385180742153 -0.0004941478 0.00038519 0.00008834 0.01650959
4 -76.385180774173 -0.0000000320 0.00007657 0.00002027 0.00029092
5 -76.385180774932 -0.0000000008 0.00000194 0.00000051 0.00002929
6 -76.385180774934 -0.0000000000 0.00000014 0.00000003 0.00000214
*** SCF converged in 6 iterations. Time: 0.41 sec.
Spin-Restricted Kohn-Sham:
--------------------------
Total Energy : -76.3851807749 a.u.
Electronic Energy : -85.5413254944 a.u.
Nuclear Repulsion Energy : 9.1561447194 a.u.
------------------------------------
Gradient Norm : 0.0000001389 a.u.
Ground State Information
------------------------
Charge of Molecule : 0.0
Multiplicity (2S+1) : 1.0
Magnetic Quantum Number (M_S) : 0.0
Spin Restricted Orbitals
------------------------
Molecular Orbital No. 1:
--------------------------
Occupation: 2.000 Energy: -19.13379 a.u.
( 1 O 1s : 1.00)
Molecular Orbital No. 2:
--------------------------
Occupation: 2.000 Energy: -1.01751 a.u.
( 1 O 1s : -0.21) ( 1 O 2s : 0.46) ( 1 O 3s : 0.45)
( 1 O 1p0 : -0.15) ( 2 H 1s : 0.15) ( 3 H 1s : 0.15)
Molecular Orbital No. 3:
--------------------------
Occupation: 2.000 Energy: -0.52917 a.u.
( 1 O 1p+1: 0.52) ( 1 O 2p+1: 0.23) ( 2 H 1s : -0.27)
( 2 H 2s : -0.15) ( 3 H 1s : 0.27) ( 3 H 2s : 0.15)
Molecular Orbital No. 4:
--------------------------
Occupation: 2.000 Energy: -0.35661 a.u.
( 1 O 2s : 0.20) ( 1 O 3s : 0.37) ( 1 O 1p0 : 0.54)
( 1 O 2p0 : 0.38)
Molecular Orbital No. 5:
--------------------------
Occupation: 2.000 Energy: -0.29214 a.u.
( 1 O 1p-1: 0.65) ( 1 O 2p-1: 0.50)
Molecular Orbital No. 6:
--------------------------
Occupation: 0.000 Energy: 0.05639 a.u.
( 1 O 2s : -0.15) ( 1 O 3s : -1.09) ( 1 O 1p0 : 0.29)
( 1 O 2p0 : 0.44) ( 2 H 2s : 0.94) ( 3 H 2s : 0.94)
Molecular Orbital No. 7:
--------------------------
Occupation: 0.000 Energy: 0.14625 a.u.
( 1 O 1p+1: 0.42) ( 1 O 2p+1: 0.75) ( 2 H 2s : 1.28)
( 3 H 2s : -1.28)
Molecular Orbital No. 8:
--------------------------
Occupation: 0.000 Energy: 0.80982 a.u.
( 1 O 1p+1: -0.20) ( 1 O 2p+1: -0.53) ( 2 H 1s : -0.97)
( 2 H 2s : 0.67) ( 3 H 1s : 0.97) ( 3 H 2s : -0.67)
Molecular Orbital No. 9:
--------------------------
Occupation: 0.000 Energy: 0.87513 a.u.
( 1 O 2s : 0.18) ( 1 O 3s : -0.28) ( 1 O 1p0 : -0.78)
( 1 O 2p0 : 0.50) ( 2 H 1s : -0.71) ( 2 H 2s : 0.59)
( 3 H 1s : -0.71) ( 3 H 2s : 0.59)
Molecular Orbital No. 10:
--------------------------
Occupation: 0.000 Energy: 0.88918 a.u.
( 1 O 1p-1: -0.96) ( 1 O 2p-1: 1.04)
Ground State Dipole Moment
----------------------------
X : -0.000000 a.u. -0.000000 Debye
Y : 0.000000 a.u. 0.000000 Debye
Z : -0.968145 a.u. -2.460780 Debye
Total : 0.968145 a.u. 2.460780 Debye
Full-space results#
For the full-space results, we construct the Hessian and property gradients:
lr_eig_solver = vlx.LinearResponseEigenSolver()
lr_eig_solver.update_settings(scf_settings, method_settings)
lr_solver = vlx.LinearResponseSolver()
lr_solver.update_settings(scf_settings, method_settings)
# Electronic Hessian
E2 = lr_eig_solver.get_e2(vlx_mol, vlx_bas, scf_results)
# Property gradients for dipole operator
V1_x, V1_y, V1_z = lr_solver.get_prop_grad("electric dipole", "xyz", vlx_mol, vlx_bas, scf_results)
# Dimension
c = int(len(E2) / 2)
# Overlap matrix
S2 = np.identity(2 * c)
S2[c : 2 * c, c : 2 * c] *= -1
* Info * Using the Libxc library (version 6.2.2).
S. Lehtola, C. Steigemann, M. J.T. Oliveira, and M. A.L. Marques., SoftwareX 7, 1–5 (2018)
* Info * Using the B3LYP functional.
P. J. Stephens, F. J. Devlin, C. F. Chabalowski, and M. J. Frisch., J. Phys. Chem. 98, 11623 (1994)
* Info * Molecular grid with 40792 points generated in 0.02 sec.
* Info * Processing Fock builds... (batch size: 160)
* Info * batch 1/1
Calculating the excitation energies and oscillator strengths:
# Set up and solve eigenvalue problem
Sinv = np.linalg.inv(S2) # for clarity - is identical
M = np.matmul(Sinv, E2)
eigs, X = np.linalg.eig(M)
# Reorder results
idx = np.argsort(eigs)
eigs = np.array(eigs)[idx]
X = np.array(X)[:, idx]
# Compute oscillator strengths
fosc = []
for i in range(int(len(eigs) / 2)):
j = i + int(len(eigs) / 2) # focus on excitations
Xf = X[:, j]
Xf = Xf / np.sqrt(np.matmul(Xf.T, np.matmul(S2, Xf)))
tm = np.dot(Xf, V1_x) ** 2 + np.dot(Xf, V1_y) ** 2 + np.dot(Xf, V1_z) ** 2
fosc.append(tm * 2.0 / 3.0 * eigs[j])
CVS-space results#
The CVS-space results can be obtained as discussed in this section, or directly using the VeloxChem implementation:
lr_eig_solver.core_excitation = True
lr_eig_solver.num_core_orbitals = 1
lr_eig_solver.nstates = 3
vlx_cvs_results = lr_eig_solver.compute(vlx_mol, vlx_bas, scf_results)
Show code cell output
Linear Response EigenSolver Setup
===================================
Number of States : 3
Max. Number of Iterations : 150
Convergence Threshold : 1.0e-06
ERI Screening Scheme : Cauchy Schwarz + Density
ERI Screening Threshold : 1.0e-12
Exchange-Correlation Functional : B3LYP
Molecular Grid Level : 4
* Info * Using the Libxc library (version 6.2.2).
S. Lehtola, C. Steigemann, M. J.T. Oliveira, and M. A.L. Marques., SoftwareX 7, 1–5 (2018)
* Info * Using the B3LYP functional.
P. J. Stephens, F. J. Devlin, C. F. Chabalowski, and M. J. Frisch., J. Phys. Chem. 98, 11623 (1994)
* Info * Molecular grid with 40792 points generated in 0.02 sec.
* Info * Processing Fock builds... (batch size: 6)
* Info * batch 1/1
* Info * 3 gerade trial vectors in reduced space
* Info * 3 ungerade trial vectors in reduced space
* Info * 1.75 kB of memory used for subspace procedure on the master node
* Info * 7.26 GB of memory available for the solver on the master node
*** Iteration: 1 * Residuals (Max,Min): 9.82e-02 and 2.73e-02
Excitation 1 : 19.11351025 Residual Norm: 0.09818089
Excitation 2 : 19.18647630 Residual Norm: 0.09204895
Excitation 3 : 19.84616908 Residual Norm: 0.02730824
* Info * Processing Fock builds... (batch size: 4)
* Info * batch 1/1
* Info * 5 gerade trial vectors in reduced space
* Info * 5 ungerade trial vectors in reduced space
* Info * 2.42 kB of memory used for subspace procedure on the master node
* Info * 7.26 GB of memory available for the solver on the master node
*** Iteration: 2 * Residuals (Max,Min): 1.01e-02 and 1.66e-14
Excitation 1 : 19.11231928 Residual Norm: 0.01012702
Excitation 2 : 19.18487023 Residual Norm: 0.00000000 converged
Excitation 3 : 19.84589976 Residual Norm: 0.00000000 converged
* Info * Processing Fock builds... (batch size: 2)
* Info * batch 1/1
* Info * 6 gerade trial vectors in reduced space
* Info * 6 ungerade trial vectors in reduced space
* Info * 2.68 kB of memory used for subspace procedure on the master node
* Info * 7.26 GB of memory available for the solver on the master node
*** Iteration: 3 * Residuals (Max,Min): 2.51e-04 and 5.08e-14
Excitation 1 : 19.11231840 Residual Norm: 0.00025135
Excitation 2 : 19.18487023 Residual Norm: 0.00000000 converged
Excitation 3 : 19.84589976 Residual Norm: 0.00000000 converged
* Info * Processing Fock builds... (batch size: 2)
* Info * batch 1/1
* Info * 7 gerade trial vectors in reduced space
* Info * 7 ungerade trial vectors in reduced space
* Info * 2.77 kB of memory used for subspace procedure on the master node
* Info * 7.26 GB of memory available for the solver on the master node
*** Iteration: 4 * Residuals (Max,Min): 4.76e-14 and 1.43e-14
Excitation 1 : 19.11231840 Residual Norm: 0.00000000 converged
Excitation 2 : 19.18487023 Residual Norm: 0.00000000 converged
Excitation 3 : 19.84589976 Residual Norm: 0.00000000 converged
*** Linear response converged in 4 iterations. Time: 0.62 sec
Electric Transition Dipole Moments (dipole length, a.u.)
--------------------------------------------------------
X Y Z
Excited State S1: -0.000000 0.000000 0.036994
Excited State S2: -0.053332 -0.000000 -0.000000
Excited State S3: 0.026326 0.000000 -0.000000
Electric Transition Dipole Moments (dipole velocity, a.u.)
----------------------------------------------------------
X Y Z
Excited State S1: -0.000000 -0.000000 0.037908
Excited State S2: -0.054574 -0.000000 -0.000000
Excited State S3: 0.023365 0.000000 0.000000
Magnetic Transition Dipole Moments (a.u.)
-----------------------------------------
X Y Z
Excited State S1: 0.000000 -0.000000 0.000000
Excited State S2: 0.000000 -0.116020 0.000000
Excited State S3: -0.000000 0.051026 -0.000000
One-Photon Absorption
---------------------
Excited State S1: 19.11231840 a.u. 520.07268 eV Osc.Str. 0.0174
Excited State S2: 19.18487023 a.u. 522.04691 eV Osc.Str. 0.0364
Excited State S3: 19.84589976 a.u. 540.03444 eV Osc.Str. 0.0092
Electronic Circular Dichroism
-----------------------------
Excited State S1: Rot.Str. 0.000000 a.u. 0.0000 [10**(-40) cgs]
Excited State S2: Rot.Str. -0.000000 a.u. -0.0000 [10**(-40) cgs]
Excited State S3: Rot.Str. -0.000000 a.u. -0.0000 [10**(-40) cgs]
Character of excitations:
Excited state 1
---------------
core_1 -> LUMO -0.9993
Excited state 2
---------------
core_1 -> LUMO+1 0.9984
Excited state 3
---------------
core_1 -> LUMO+2 0.9986
Comparison#
Comparing the obtained spectra:
plt.figure(figsize=(6,3))
x, y = eigs[int(len(eigs) / 2) :], fosc
x1, y1 = lorentzian(x, y, 518 / au2ev, 525 / au2ev, 0.001, 0.3 / au2ev)
plt.plot(x1 * au2ev, y1)
x, y = vlx_cvs_results['eigenvalues'], vlx_cvs_results['oscillator_strengths']
x2, y2 = lorentzian(x, y, 518 / au2ev, 525 / au2ev, 0.001, 0.3 / au2ev)
plt.plot(x2 * au2ev, y2, linestyle='--')
plt.plot(x1 * au2ev, 10*(y1 - y2), linestyle=':')
plt.legend(("Full-space", "CVS-space", "Difference x10"))
plt.tight_layout()
plt.show()
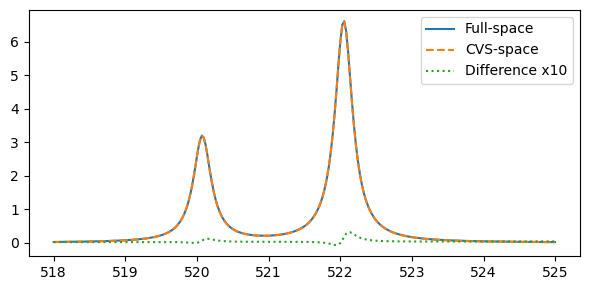
We note a small difference between the two approaches. This difference has some dependence on the basis set, but will continue to be small for the K-edge.
Ionization energies from XAS#
Can model the ionization energy by targetting excitations to extremely diffuse molecular orbital. Here: consider both spectrum and IE of water, at a CVS-ADC(2)-x/6-31G[+diffuse] level of theory.
To be added
Ionization energies from XES#
Can model the ionization energy by targetting decays from an extremely diffuse molecular orbital, with a core-electron already moved to it. The need of preparing this state makes the approach rather useless, but it can still provide insight into relaxation effects of XES. Here: consider the IE of water, at a CVS-ADC(2)/6-31G[+diffuse] level of theory.
To be added
XES considered in reverse#
Instead of modeling XES by looking at the (negative) eigenstates of a core-hole reference state, it is possible to use a valence-hole reference state, and then consider core-excitations into this hole. This thus models the XES process more from the point of view of XAS, i.e. in reverse. However, this approach presupposes:
That a single-particle picture works quite well, and that specific valence-hole will yield reasonable representations of the valence-hole left following decay into a core-hole
That the valence-hole can be converged well, and that the different (non-orthogonal) reference states from each calculation are sufficiently consistent with each other
Furthermore, the calculation is made more tedious, as
It requires one explicit calculation per state
As such, this approach is by not suggested for practical calculations, but it does illustrate the ease of which such exotic calculations can be run, as well as teach us something about the relaxation of core-transitions.
Considering the X-ray emission spectra of water, we create valence-holes in the four frontier valence MOs and construct a spectrum from this:
Note
pyscf version - to be changed
# Containers for resulting energies and intensities
xes_rev_E = []
xes_rev_f = []
# Perform unrestricted SCF calculation
scf_res = scf.UHF(mol)
scf_res.kernel()
# Copy molecular orbital coefficients
mo0 = copy.deepcopy(scf_res.mo_coeff)
# Reference calculation from core-hole
occ0 = copy.deepcopy(scf_res.mo_occ)
occ0[0][0] = 0.0
scf_ion = scf.UHF(mol)
scf.addons.mom_occ(scf_ion, mo0, occ0)
scf_ion.kernel()
adc_xes = adcc.adc2(scf_ion, n_states=4)
xes_E = -au2ev * adc_xes.excitation_energy
xes_f = adc_xes.oscillator_strength
for i in range(4):
occ0 = copy.deepcopy(scf_res.mo_occ)
occ0[0][4 - i] = 0.0
# Perform unrestricted SCF calculation with MOM constraint
scf_ion = scf.UHF(mol)
scf.addons.mom_occ(scf_ion, mo0, occ0)
scf_ion.kernel()
# Perform ADC calculation of first four states
adc_xes = adcc.cvs_adc2(scf_ion, n_states=1, core_orbitals=1)
xes_rev_E.append(au2ev * adc_xes.excitation_energy)
xes_rev_f.append(adc_xes.oscillator_strength)
Comparing the two different spectra:
plt.figure(figsize=(6, 3))
xi, yi = lorentzian(xes_E, xes_f, 518, 534, 0.01, 0.5)
plt.plot(xi, yi)
xi, yi = lorentzian(xes_rev_E, xes_rev_f, 518, 534, 0.01, 0.5)
plt.plot(xi, yi)
plt.legend(("From core-hole", "From valence-hole"))
plt.tight_layout()
plt.show()
