Analysis#
The breakdown of spectra into the Cartesian components, as well as decomposing to occupied MOs is discussed in the X-ray section. The study of excited states using natural transition orbitals and detachment/attachment densities are currently in the visualization section, and here we will now focus on using OrbitalViewer and decomposition of eigenstates.
Show code cell source
import copy
import gator
import matplotlib.pyplot as plt
import numpy as np
import veloxchem as vlx
# for vlx
silent_ostream = vlx.OutputStream(None)
from mpi4py import MPI
comm = MPI.COMM_WORLD
# au to eV conversion factor
au2ev = 27.211386
def lorentzian(x, y, xmin, xmax, xstep, gamma):
"""
Lorentzian broadening function
Call: xi,yi = lorentzian(energies, intensities, start energy, end energy, energy step, gamma)
"""
xi = np.arange(xmin, xmax, xstep)
yi = np.zeros(len(xi))
for i in range(len(xi)):
for k in range(len(x)):
yi[i] = yi[i] + y[k] * (gamma / 2.0) / (
(xi[i] - x[k]) ** 2 + (gamma / 2.0) ** 2
)
return xi, yi
First, we calculate the six lowest states of methanol using ADC(2):
ch3oh_mol_str = '''
C 0.6627602692 -0.0195253241 -0.0000000000
O -0.7482324502 0.1217146925 0.0000000000
H 1.0282229693 -0.5397922417 -0.8872632580
H 1.0282229693 -0.5397922417 0.8872632580
H 1.0781531801 0.9835591659 -0.0000000000
H -1.1253011321 -0.7605402778 0.0000000000
'''
# Construct structure and basis objects
struct = gator.get_molecule(ch3oh_mol_str)
basis = gator.get_molecular_basis(struct, "6-31G")
# Perform SCF calculation
scf_gs = gator.run_scf(struct, basis)
# Calculate the 6 lowest eigenstates
adc_res = gator.run_adc(struct, basis, scf_gs, method="adc2", singlets=6)
Show code cell output
* Info * Reading basis set from file: /home/emi/miniconda3/envs/echem/lib/python3.11/site-packages/veloxchem/basis/6-31G
Molecular Basis (Atomic Basis)
================================
Basis: 6-31G
Atom Contracted GTOs Primitive GTOs
O (3S,2P) (10S,4P)
H (2S) (4S)
C (3S,2P) (10S,4P)
Contracted Basis Functions : 26
Primitive Basis Functions : 60
Self Consistent Field Driver Setup
====================================
Wave Function Model : Spin-Restricted Hartree-Fock
Initial Guess Model : Superposition of Atomic Densities
Convergence Accelerator : Two Level Direct Inversion of Iterative Subspace
Max. Number of Iterations : 50
Max. Number of Error Vectors : 10
Convergence Threshold : 1.0e-06
ERI Screening Scheme : Cauchy Schwarz + Density
ERI Screening Mode : Dynamic
ERI Screening Threshold : 1.0e-12
Linear Dependence Threshold : 1.0e-06
* Info * Nuclear repulsion energy: 40.3876414915 a.u.
* Info * Overlap matrix computed in 0.00 sec.
* Info * Kinetic energy matrix computed in 0.00 sec.
* Info * Nuclear potential matrix computed in 0.00 sec.
* Info * Orthogonalization matrix computed in 0.00 sec.
* Info * SAD initial guess computed in 0.02 sec.
* Info * Starting Reduced Basis SCF calculation...
* Info * ...done. SCF energy in reduced basis set: -114.986646483208 a.u. Time: 0.08 sec.
* Info * Overlap matrix computed in 0.00 sec.
* Info * Kinetic energy matrix computed in 0.00 sec.
* Info * Nuclear potential matrix computed in 0.00 sec.
* Info * Orthogonalization matrix computed in 0.00 sec.
Iter. | Hartree-Fock Energy | Energy Change | Gradient Norm | Max. Gradient | Density Change
--------------------------------------------------------------------------------------------
1 -114.986647455185 0.0000000000 0.00019765 0.00003189 0.00000000
2 -114.986647466155 -0.0000000110 0.00008804 0.00001229 0.00014964
3 -114.986647467681 -0.0000000015 0.00001316 0.00000245 0.00005028
4 -114.986647467711 -0.0000000000 0.00000768 0.00000123 0.00000788
5 -114.986647467718 -0.0000000000 0.00000092 0.00000020 0.00000271
*** SCF converged in 5 iterations. Time: 0.06 sec.
Spin-Restricted Hartree-Fock:
-----------------------------
Total Energy : -114.9866474677 a.u.
Electronic Energy : -155.3742889592 a.u.
Nuclear Repulsion Energy : 40.3876414915 a.u.
------------------------------------
Gradient Norm : 0.0000009201 a.u.
Ground State Information
------------------------
Charge of Molecule : 0.0
Multiplicity (2S+1) : 1.0
Magnetic Quantum Number (M_S) : 0.0
Spin Restricted Orbitals
------------------------
Molecular Orbital No. 5:
--------------------------
Occupation: 2.000 Energy: -0.68674 a.u.
( 1 C 1p+1: 0.18) ( 1 C 1p-1: -0.23) ( 2 O 3s : -0.17)
( 2 O 1p+1: -0.23) ( 2 O 1p-1: -0.36) ( 2 O 2p-1: -0.20)
( 6 H 1s : 0.23)
Molecular Orbital No. 6:
--------------------------
Occupation: 2.000 Energy: -0.62359 a.u.
( 1 C 1p0 : 0.38) ( 1 C 2p0 : 0.18) ( 2 O 1p0 : 0.33)
( 2 O 2p0 : 0.22) ( 3 H 1s : -0.19) ( 4 H 1s : 0.19)
Molecular Orbital No. 7:
--------------------------
Occupation: 2.000 Energy: -0.58786 a.u.
( 1 C 1p+1: -0.30) ( 1 C 1p-1: -0.25) ( 1 C 2p-1: -0.16)
( 2 O 1p+1: 0.38) ( 2 O 2p+1: 0.27) ( 5 H 1s : -0.22)
Molecular Orbital No. 8:
--------------------------
Occupation: 2.000 Energy: -0.49474 a.u.
( 1 C 1p-1: -0.30) ( 2 O 3s : 0.21) ( 2 O 1p+1: -0.19)
( 2 O 1p-1: 0.39) ( 2 O 2p+1: -0.16) ( 2 O 2p-1: 0.30)
( 5 H 1s : -0.20) ( 5 H 2s : -0.18)
Molecular Orbital No. 9:
--------------------------
Occupation: 2.000 Energy: -0.44686 a.u.
( 1 C 1p0 : -0.24) ( 2 O 1p0 : 0.55) ( 2 O 2p0 : 0.46)
( 3 H 1s : 0.17) ( 3 H 2s : 0.19) ( 4 H 1s : -0.17)
( 4 H 2s : -0.19)
Molecular Orbital No. 10:
--------------------------
Occupation: 0.000 Energy: 0.21888 a.u.
( 1 C 3s : -1.06) ( 1 C 1p+1: -0.16) ( 1 C 2p+1: -0.60)
( 2 O 3s : -0.96) ( 2 O 1p-1: 0.20) ( 2 O 2p-1: 0.44)
( 3 H 2s : 0.63) ( 4 H 2s : 0.63) ( 5 H 2s : 0.47)
( 6 H 2s : 1.21)
Molecular Orbital No. 11:
--------------------------
Occupation: 0.000 Energy: 0.27257 a.u.
( 1 C 3s : 2.41) ( 1 C 2p+1: 0.17) ( 2 O 3s : -0.77)
( 2 O 2p+1: -0.17) ( 2 O 2p-1: 0.30) ( 3 H 2s : -1.11)
( 4 H 2s : -1.11) ( 5 H 2s : -1.04) ( 6 H 2s : 0.73)
Molecular Orbital No. 12:
--------------------------
Occupation: 0.000 Energy: 0.31271 a.u.
( 1 C 1p-1: 0.33) ( 1 C 2p+1: 0.39) ( 1 C 2p-1: 1.45)
( 2 O 2p+1: 0.17) ( 2 O 2p-1: -0.16) ( 3 H 2s : 0.83)
( 4 H 2s : 0.83) ( 5 H 2s : -1.98) ( 6 H 2s : 0.21)
Molecular Orbital No. 13:
--------------------------
Occupation: 0.000 Energy: 0.32064 a.u.
( 1 C 1p0 : 0.37) ( 1 C 2p0 : 1.49) ( 2 O 2p0 : -0.25)
( 3 H 2s : 1.67) ( 4 H 2s : -1.67)
Molecular Orbital No. 14:
--------------------------
Occupation: 0.000 Energy: 0.37611 a.u.
( 1 C 3s : -0.88) ( 1 C 1p+1: 0.20) ( 1 C 2p+1: 1.53)
( 1 C 2p-1: -0.50) ( 2 O 3s : 0.76) ( 2 O 1p+1: 0.32)
( 2 O 2p+1: 0.97) ( 2 O 2p-1: 0.29) ( 3 H 2s : -0.35)
( 4 H 2s : -0.35) ( 5 H 2s : 0.33) ( 6 H 2s : 0.97)
Ground State Dipole Moment
----------------------------
X : 0.513109 a.u. 1.304192 Debye
Y : -0.771457 a.u. -1.960848 Debye
Z : 0.000000 a.u. 0.000000 Debye
Total : 0.926513 a.u. 2.354961 Debye
SCF converged in 5 iterations.
Total Energy: -114.9866474677 au
Starting adc2 singlet Jacobi-Davidson ...
Niter n_ss max_residual time Ritz values
1 12 0.23909 112ms [0.40241316 0.48084642 0.51034518 0.52072285 0.55248738 0.55772689]
2 24 0.010561 224ms [0.29557131 0.37845885 0.39618815 0.4170348 0.44699784 0.45009195]
3 36 0.0038423 317ms [0.29423544 0.37469582 0.38629969 0.41095523 0.43604013 0.43686795]
4 48 0.00035144 398ms [0.29417706 0.37426126 0.38422222 0.40954519 0.43305633 0.43490802]
5 60 1.7396e-05 483ms [0.29417387 0.37422958 0.38413954 0.40949836 0.43288848 0.43484835]
=== Restart ===
6 24 3.5709e-06 420ms [0.29417373 0.37422705 0.3841368 0.40949611 0.4328759 0.43484511]
7 36 3.3958e-07 346ms [0.29417371 0.37422666 0.38413652 0.40949598 0.43287347 0.43484478]
=== Converged ===
Number of matrix applies: 84
Total solver time: 2s 328ms
Print and plot spectra#
Resulting eigenstates can be summarized with describe():
print(adc_res.describe())
+--------------------------------------------------------------+
| adc2 singlet , converged |
+--------------------------------------------------------------+
| # excitation energy osc str |v1|^2 |v2|^2 |
| (au) (eV) |
| 0 0.2941737 8.004874 0.0000 0.9527 0.04731 |
| 1 0.3742267 10.18323 0.0109 0.9533 0.04671 |
| 2 0.3841365 10.45289 0.0868 0.9329 0.06713 |
| 3 0.409496 11.14295 0.0005 0.9455 0.05445 |
| 4 0.4328735 11.77909 0.1071 0.9252 0.07478 |
| 5 0.4348448 11.83273 0.0266 0.9439 0.05607 |
+--------------------------------------------------------------+
And plotted with built-in functionalities, and here we also plot the state number next to each state to simplify analysis (note indexing from 0):
plt.figure(figsize=(6,4))
adc_res.plot_spectrum()
for i in np.arange(len(adc_res.excitation_energy)):
plt.text(au2ev*adc_res.excitation_energy[i]+0.01,adc_res.oscillator_strength[i]/6.5,str(i),color='r')
plt.tight_layout()
plt.show()
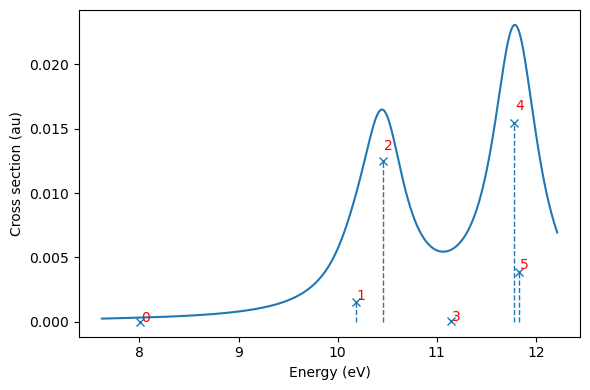
Dominant contributions to eigenstates#
With describe_amplitudes we can study the dominant contributions of the states:
print(adc_res.describe_amplitudes())
+-------------------------------------------------------+
| State 0 , 0.2941737 au, 8.004874 eV |
+-------------------------------------------------------+
| HOMO -> LUMO a ->a -0.652 |
| HOMO -3 -> LUMO a ->a -0.153 |
| HOMO -> LUMO +1 a ->a -0.146 |
| HOMO -3 -> LUMO +1 a ->a -0.0575 |
| HOMO -> LUMO +8 a ->a +0.0233 |
| HOMO -3 -> LUMO +4 a ->a -0.0232 |
| HOMO -> LUMO+15 a ->a +0.0206 |
| HOMO -> LUMO+10 a ->a +0.0196 |
| HOMO -> LUMO+12 a ->a +0.0175 |
| HOMO -> LUMO +7 a ->a +0.0165 |
| HOMO -> LUMO +2 a ->a +0.0105 |
| HOMO -4 HOMO -> LUMO +4 LUMO ab->ab -0.0157 |
| HOMO HOMO -> LUMO LUMO+13 ab->ab -0.014 |
| HOMO -4 HOMO -> LUMO LUMO ab->ab -0.0139 |
| HOMO -2 HOMO -> LUMO +4 LUMO ab->ab +0.012 |
| HOMO -6 HOMO -> LUMO LUMO ab->ab +0.0117 |
| HOMO -1 HOMO -> LUMO LUMO+10 aa->aa +0.0116 |
| HOMO -3 HOMO -2 -> LUMO LUMO +4 ab->ab +0.011 |
| HOMO HOMO -1 -> LUMO LUMO+10 ab->ab -0.0109 |
+-------------------------------------------------------+
| State 1 , 0.3742267 au, 10.18323 eV |
+-------------------------------------------------------+
| HOMO -1 -> LUMO a ->a -0.648 |
| HOMO -2 -> LUMO a ->a +0.156 |
| HOMO -1 -> LUMO +1 a ->a -0.1 |
| HOMO -4 -> LUMO a ->a +0.0798 |
| HOMO -2 -> LUMO +1 a ->a +0.0596 |
| HOMO -2 -> LUMO +4 a ->a +0.046 |
| HOMO -1 -> LUMO +4 a ->a +0.0456 |
| HOMO -> LUMO +3 a ->a -0.0436 |
| HOMO -4 -> LUMO +1 a ->a +0.0369 |
| HOMO -1 -> LUMO +2 a ->a +0.0291 |
| HOMO -5 -> LUMO a ->a -0.0278 |
| HOMO -1 -> LUMO +7 a ->a +0.0198 |
| HOMO -1 -> LUMO+12 a ->a +0.0198 |
| HOMO -1 -> LUMO +8 a ->a +0.0159 |
| HOMO -6 -> LUMO a ->a +0.015 |
| HOMO -2 -> LUMO +2 a ->a +0.0133 |
| HOMO -2 -> LUMO+15 a ->a -0.0126 |
| HOMO -> LUMO+13 a ->a -0.0126 |
| HOMO -1 -> LUMO+15 a ->a +0.0116 |
| HOMO -4 HOMO -1 -> LUMO LUMO ab->ab -0.0187 |
| HOMO -1 HOMO -1 -> LUMO LUMO ab->ab +0.0152 |
| HOMO -4 HOMO -2 -> LUMO LUMO +4 aa->aa -0.0146 |
| HOMO -4 HOMO -1 -> LUMO +4 LUMO ab->ab -0.0118 |
| HOMO -1 HOMO -1 -> LUMO LUMO +1 ab->ab +0.0102 |
+-------------------------------------------------------+
| State 2 , 0.3841365 au, 10.45289 eV |
+-------------------------------------------------------+
| HOMO -> LUMO +1 a ->a +0.64 |
| HOMO -> LUMO a ->a -0.152 |
| HOMO -> LUMO +2 a ->a -0.11 |
| HOMO -> LUMO +4 a ->a -0.0918 |
| HOMO -3 -> LUMO +1 a ->a +0.0871 |
| HOMO -> LUMO +7 a ->a -0.0437 |
| HOMO -3 -> LUMO +7 a ->a -0.0258 |
| HOMO -> LUMO+10 a ->a -0.0214 |
| HOMO -> LUMO+11 a ->a -0.0192 |
| HOMO -> LUMO+12 a ->a +0.0176 |
| HOMO -3 -> LUMO +4 a ->a -0.0167 |
| HOMO -3 -> LUMO a ->a +0.0165 |
| HOMO -3 -> LUMO +2 a ->a -0.0139 |
| HOMO HOMO -> LUMO +1 LUMO +3 ab->ab +0.0199 |
| HOMO -4 HOMO -> LUMO +4 LUMO +1 ab->ab +0.018 |
| HOMO -2 HOMO -> LUMO +4 LUMO +1 ab->ab -0.0179 |
| HOMO HOMO -> LUMO +1 LUMO+13 ab->ab +0.016 |
| HOMO -2 HOMO -> LUMO +1 LUMO +4 aa->aa +0.0157 |
| HOMO -4 HOMO -> LUMO +1 LUMO +4 aa->aa -0.0149 |
| HOMO -1 HOMO -> LUMO +1 LUMO+10 aa->aa -0.0122 |
| HOMO -3 HOMO -2 -> LUMO +1 LUMO +4 ab->ab -0.0121 |
| HOMO -4 HOMO -3 -> LUMO +1 LUMO +4 aa->aa -0.0113 |
| HOMO -4 HOMO -3 -> LUMO +4 LUMO +1 ab->ab +0.0111 |
| HOMO HOMO -1 -> LUMO +1 LUMO+10 ab->ab +0.0111 |
| HOMO -1 HOMO -> LUMO +2 LUMO +1 ab->ab +0.011 |
| HOMO -3 HOMO -2 -> LUMO +1 LUMO +4 aa->aa -0.0109 |
+-------------------------------------------------------+
| State 3 , 0.409496 au, 11.14295 eV |
+-------------------------------------------------------+
| HOMO -> LUMO +2 a ->a -0.529 |
| HOMO -> LUMO +4 a ->a -0.389 |
| HOMO -> LUMO +1 a ->a -0.137 |
| HOMO -> LUMO +7 a ->a -0.0715 |
| HOMO -3 -> LUMO +4 a ->a -0.0705 |
| HOMO -3 -> LUMO +2 a ->a -0.0628 |
| HOMO -3 -> LUMO a ->a -0.0623 |
| HOMO -> LUMO a ->a +0.0354 |
| HOMO -3 -> LUMO +1 a ->a -0.03 |
| HOMO -> LUMO+15 a ->a +0.0261 |
| HOMO -> LUMO +8 a ->a +0.0239 |
| HOMO -> LUMO+14 a ->a +0.0175 |
| HOMO -> LUMO+12 a ->a -0.0152 |
| HOMO -3 -> LUMO +7 a ->a -0.0151 |
| HOMO -2 -> LUMO +3 a ->a +0.0113 |
| HOMO -3 -> LUMO+11 a ->a -0.0108 |
| HOMO -> LUMO+10 a ->a -0.0108 |
| HOMO -2 HOMO -> LUMO +4 LUMO +2 ab->ab +0.0148 |
| HOMO -4 HOMO -> LUMO +4 LUMO +2 ab->ab -0.0138 |
| HOMO HOMO -> LUMO +2 LUMO+13 ab->ab -0.013 |
| HOMO -4 HOMO -> LUMO +2 LUMO +4 aa->aa +0.0121 |
| HOMO -2 HOMO -> LUMO +2 LUMO +4 aa->aa -0.0106 |
| HOMO -3 HOMO -2 -> LUMO +2 LUMO +4 ab->ab +0.0105 |
| HOMO -4 HOMO -3 -> LUMO +2 LUMO +4 aa->aa +0.0102 |
| HOMO -1 HOMO -> LUMO +2 LUMO +2 ab->ab -0.0101 |
+-------------------------------------------------------+
| State 4 , 0.4328735 au, 11.77909 eV |
+-------------------------------------------------------+
| HOMO -> LUMO +3 a ->a +0.652 |
| HOMO -3 -> LUMO +3 a ->a +0.119 |
| HOMO -1 -> LUMO +1 a ->a +0.0857 |
| HOMO -1 -> LUMO +2 a ->a -0.0766 |
| HOMO -1 -> LUMO a ->a -0.0627 |
| HOMO -2 -> LUMO +4 a ->a +0.0411 |
| HOMO -> LUMO +9 a ->a -0.03 |
| HOMO -2 -> LUMO +1 a ->a -0.027 |
| HOMO -> LUMO +6 a ->a -0.022 |
| HOMO -4 -> LUMO a ->a -0.0202 |
| HOMO -3 -> LUMO +9 a ->a -0.0147 |
| HOMO -> LUMO+13 a ->a -0.0144 |
| HOMO -1 -> LUMO+10 a ->a -0.0144 |
| HOMO -2 -> LUMO +5 a ->a -0.0122 |
| HOMO -4 -> LUMO +1 a ->a -0.0116 |
| HOMO -1 -> LUMO +4 a ->a -0.0115 |
| HOMO -5 -> LUMO a ->a -0.0105 |
| HOMO HOMO -> LUMO +3 LUMO +3 ab->ab +0.0346 |
| HOMO -4 HOMO -> LUMO +4 LUMO +3 ab->ab +0.0197 |
| HOMO -2 HOMO -> LUMO +4 LUMO +3 ab->ab -0.0194 |
| HOMO -2 HOMO -> LUMO +3 LUMO +4 aa->aa +0.0183 |
| HOMO HOMO -> LUMO +3 LUMO+13 ab->ab +0.0178 |
| HOMO -4 HOMO -> LUMO +3 LUMO +4 aa->aa -0.0163 |
| HOMO -3 HOMO -> LUMO +3 LUMO +9 ab->ab -0.0143 |
| HOMO -3 HOMO -2 -> LUMO +3 LUMO +4 ab->ab -0.0132 |
| HOMO -3 HOMO -2 -> LUMO +3 LUMO +4 aa->aa -0.0126 |
| HOMO -1 HOMO -> LUMO +3 LUMO+10 aa->aa -0.0126 |
| HOMO HOMO -1 -> LUMO +3 LUMO+10 ab->ab +0.0122 |
| HOMO -4 HOMO -3 -> LUMO +3 LUMO +4 aa->aa -0.0122 |
| HOMO -4 HOMO -3 -> LUMO +4 LUMO +3 ab->ab +0.0121 |
| HOMO HOMO -> LUMO +3 LUMO +6 ab->ab +0.0119 |
| HOMO -2 HOMO -> LUMO +7 LUMO +3 ab->ab -0.0117 |
| HOMO -3 HOMO -> LUMO +3 LUMO +3 ab->ab +0.0104 |
| HOMO -2 HOMO -> LUMO +3 LUMO +7 aa->aa +0.0103 |
| HOMO -6 HOMO -> LUMO LUMO +3 ab->ab -0.0101 |
+-------------------------------------------------------+
| State 5 , 0.4348448 au, 11.83273 eV |
+-------------------------------------------------------+
| HOMO -> LUMO +4 a ->a -0.53 |
| HOMO -> LUMO +2 a ->a +0.404 |
| HOMO -3 -> LUMO +4 a ->a -0.103 |
| HOMO -> LUMO +7 a ->a -0.0685 |
| HOMO -1 -> LUMO +3 a ->a -0.0624 |
| HOMO -3 -> LUMO a ->a -0.0513 |
| HOMO -3 -> LUMO +2 a ->a +0.0464 |
| HOMO -> LUMO +5 a ->a +0.0256 |
| HOMO -> LUMO+14 a ->a +0.0242 |
| HOMO -> LUMO+10 a ->a +0.023 |
| HOMO -> LUMO+11 a ->a -0.0203 |
| HOMO -3 -> LUMO +7 a ->a -0.0194 |
| HOMO -> LUMO+15 a ->a +0.0167 |
| HOMO -> LUMO +8 a ->a -0.0164 |
| HOMO -4 -> LUMO +3 a ->a -0.0159 |
| HOMO -> LUMO a ->a +0.0133 |
| HOMO -4 HOMO -> LUMO +4 LUMO +2 ab->ab +0.0135 |
| HOMO -2 HOMO -> LUMO +2 LUMO +4 aa->aa +0.013 |
| HOMO -4 HOMO -> LUMO +4 LUMO +4 ab->ab -0.0129 |
| HOMO -2 HOMO -> LUMO +4 LUMO +2 ab->ab -0.0125 |
| HOMO -4 HOMO -> LUMO +2 LUMO +4 aa->aa -0.0121 |
| HOMO HOMO -> LUMO +2 LUMO+13 ab->ab +0.0119 |
| HOMO -2 HOMO -> LUMO +4 LUMO +4 ab->ab +0.0115 |
| HOMO -3 HOMO -2 -> LUMO +2 LUMO +4 aa->aa -0.0112 |
This outputs a string with all transitions and all contributions with an absolute value of 0.01. The printing threshold can be changed, as can the format of the output, but for now we focus on narrowing down on the two strongest state (2 and 4). This can be done by splitting the string at double line-breaks, where we also include a higher tolerance of inclusion of 0.1:
split_res = adc_res.describe_amplitudes(tolerance=0.1).split('\n\n')
Printing the dominant amplitudes of states 2 and 4:
print(split_res[2])
print('\n')
print(split_res[4])
+---------------------------------------------------+
| State 2 , 0.3841365 au, 10.45289 eV |
+---------------------------------------------------+
| HOMO -> LUMO+1 a ->a +0.64 |
| HOMO -> LUMO a ->a -0.152 |
| HOMO -> LUMO+2 a ->a -0.11 |
+---------------------------------------------------+
| State 4 , 0.4328735 au, 11.77909 eV |
+---------------------------------------------------+
| HOMO -> LUMO+3 a ->a +0.652 |
| HOMO-3 -> LUMO+3 a ->a +0.119 |
We see that both these excitations are dominate by transitions from HOMO to LUMO+1 and LUMO+3, and from describe() above we note that the transitions are dominated by singly excited configurations (\(|v^2|^2\sim0.07\)).
Visualizing molecular orbitals#
Using OrbitalViewer, we can look at HOMO, LUMO+1, and LUMO+3:
viewer = vlx.OrbitalViewer()
viewer.plot(struct, basis, scf_gs.mol_orbs)
And we obtain:
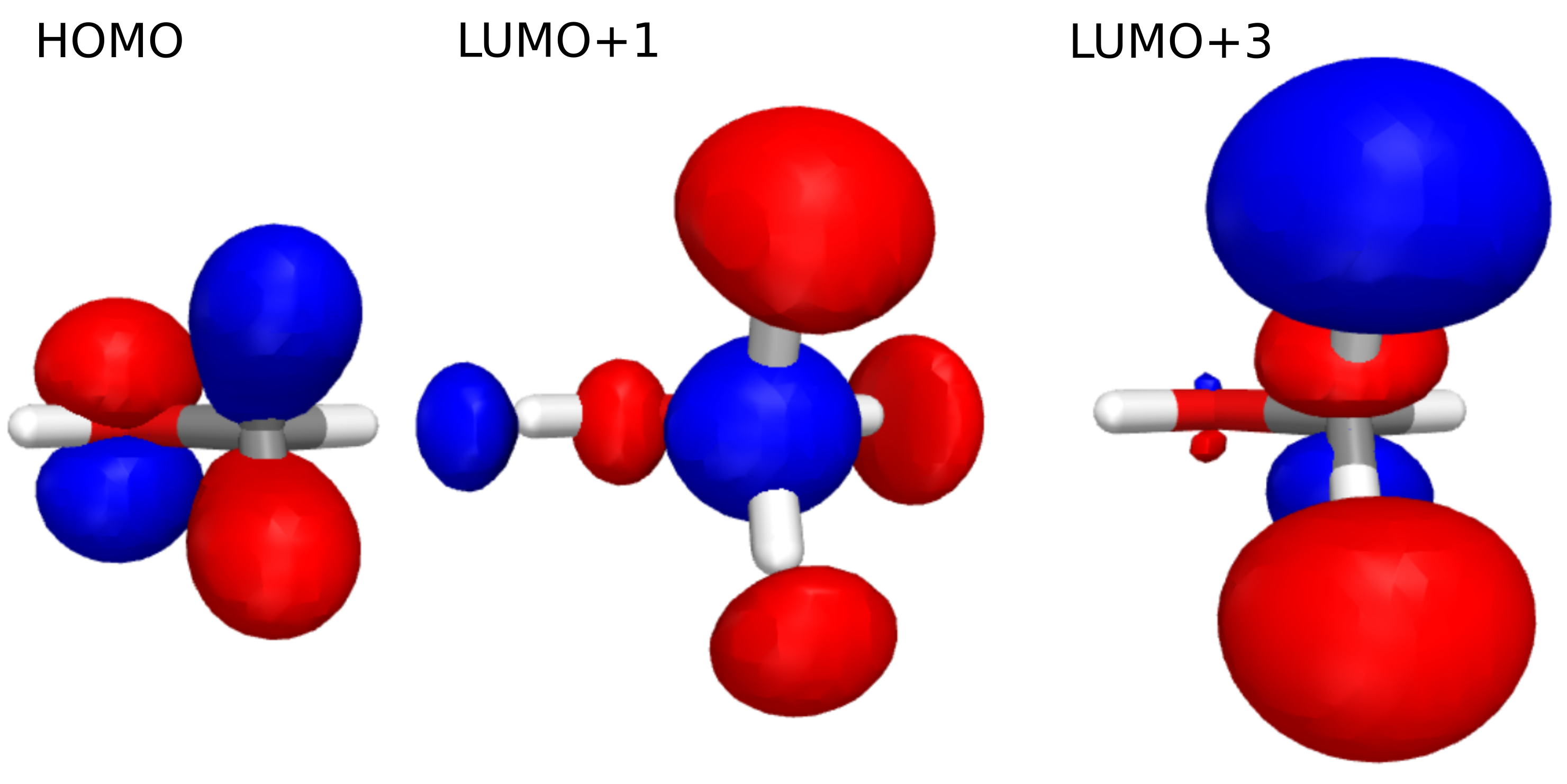
Using these MOs and above eigenstate contributions we can assign the features, provided that the excited states are relatively dominated by a few contributions, and the canonical MOs can be assigned. If this is not viable, we would instead turn to, e.g., natural transition orbitals, where we obtain a compact description of the excited states.
Polarization dependence#
Finally, we can look at the Cartesian components of the transition dipole moments, to see how the excitation is polarized:
print('State 2:',adc_res.transition_dipole_moment[2])
print('State 4:',adc_res.transition_dipole_moment[4])
State 2: [ 2.62076403e-14 -5.37675159e-14 5.82241208e-01]
State 4: [ 5.17627387e-01 -3.21072518e-01 3.00896195e-13]